Data Understanding.ipynb

{
 "cells": [
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "### Data Understanding\n",
    "- The most time consuming job in the data science is understanding the data.\n",
    "\n",
    "### What do you mean by understanding the data?\n",
    "- To understand the charactertics/attributes of the data.\n",
    "- To understand the data volumn and variables used in the data.\n",
    "\n",
    "- To understand the problems in the data such as missing value, outliers etc.\n",
    "- Data visulization is used to visualize the data and validate the attributes of the data.\n",
    "- It also helps in understand the summary of the data and glitches of the data."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "### Data Attributes:\n",
    "**Continuous Variables** - The values of the variable are in range or continuous values.\n",
    "\n",
    "**Categorical Variables** - The values of the variable are some set of values such as male or female, directions(east, west, north, south) etc.\n",
    "\n",
    "![Variable](https://user-images.githubusercontent.com/8953894/58531866-4cea0b00-81d3-11e9-96ae-c0a3e04c9a0b.png)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "notes"
    }
   },
   "source": [
    "\n",
    "- Nominal = Unordered values to the categorical variables. Ex. Gender has two categories like Male or Female.\n",
    "- Ordinal = Ordered values to the categorical variables. Ex. Low, Medium, High."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 1,
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "    User ID  Gender  Age  EstimatedSalary Country  Purchased\n",
      "0  15624510    Male   19          19000.0      UK          0\n",
      "1  15810944    Male   35          20000.0     NaN          0\n",
      "2  15668575  Female   26          43000.0   India          0\n",
      "3  15603246  Female   27          57000.0      US          0\n",
      "4  15804002    Male   19          76000.0      UK          0\n",
      "\n",
      "Shape of the data:  (400, 6)\n",
      "\n",
      "Target variable classes:  [0 1]\n"
     ]
    }
   ],
   "source": [
    "import pandas as pd\n",
    "import numpy as np\n",
    "\n",
    "df = pd.read_csv('Social_Network_Ads1.csv')\n",
    "print(df.head())\n",
    "print('\\nShape of the data: ', df.shape)\n",
    "print('\\nTarget variable classes: ', df['Purchased'].unique())"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "**Mean** = It is used to find the average of the numeric values.\n",
    "\n",
    "**Median** = It is the middle value of the sorted values. It can be used even you column/feature has outliers.\n",
    "\n",
    "**Mode** = It is the value that occurs more often.\n",
    "\n",
    "**Standard Deviation** = It measures the spread of the distribution of the data. Lower the value of standard deviation, closer it is towards the mean or expected value. It tells how far the value is from the mean. It is the square root of the variance.\n",
    "\n",
    "**Inter-Quartile Range:** It is the difference between Q3 and Q1 quartiles. The IQR is often seen as a better measure of spread than the range as it is not affected by outliers.\n",
    "\n",
    "**IQ1(25%)** = It is the middle value between the smallest and median of the data set.\n",
    "\n",
    "**IQ2(50%)** = It is the median of the data set.\n",
    "\n",
    "**IQ3(75%)** = It is the middle value between the median and largest value of the data set.\n",
    "\n",
    "**IQ4(100%)** = It is maximum value in the data set."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "notes"
    }
   },
   "source": [
    "A slightly harder, real-life example: The average height for grown men in the United States is 70\", with a standard deviation of 3\". A standard deviation of 3” means that most men (about 68%, assuming a normal distribution) have a height 3\" taller to 3” shorter than the average (67\"–73\") — one standard deviation. Almost all men (about 95%) have a height 6” taller to 6” shorter than the average (64\"–76\") — two standard deviations. Three standard deviations include all the numbers for 99.7% of the sample population being studied. This is true if the distribution is normal (bell-shaped)."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 2,
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "outputs": [
    {
     "data": {
      "text/html": [
       "<div>\n",
       "<style scoped>\n",
       "    .dataframe tbody tr th:only-of-type {\n",
       "        vertical-align: middle;\n",
       "    }\n",
       "\n",
       "    .dataframe tbody tr th {\n",
       "        vertical-align: top;\n",
       "    }\n",
       "\n",
       "    .dataframe thead th {\n",
       "        text-align: right;\n",
       "    }\n",
       "</style>\n",
       "<table border=\"1\" class=\"dataframe\">\n",
       "  <thead>\n",
       "    <tr style=\"text-align: right;\">\n",
       "      <th></th>\n",
       "      <th>User ID</th>\n",
       "      <th>Age</th>\n",
       "      <th>EstimatedSalary</th>\n",
       "      <th>Purchased</th>\n",
       "    </tr>\n",
       "  </thead>\n",
       "  <tbody>\n",
       "    <tr>\n",
       "      <th>count</th>\n",
       "      <td>4.000000e+02</td>\n",
       "      <td>400.000000</td>\n",
       "      <td>398.000000</td>\n",
       "      <td>400.000000</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>mean</th>\n",
       "      <td>1.569154e+07</td>\n",
       "      <td>37.655000</td>\n",
       "      <td>69987.437186</td>\n",
       "      <td>0.357500</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>std</th>\n",
       "      <td>7.165832e+04</td>\n",
       "      <td>10.482877</td>\n",
       "      <td>34005.146195</td>\n",
       "      <td>0.479864</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>min</th>\n",
       "      <td>1.556669e+07</td>\n",
       "      <td>18.000000</td>\n",
       "      <td>15000.000000</td>\n",
       "      <td>0.000000</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>25%</th>\n",
       "      <td>1.562676e+07</td>\n",
       "      <td>29.750000</td>\n",
       "      <td>43250.000000</td>\n",
       "      <td>0.000000</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>50%</th>\n",
       "      <td>1.569434e+07</td>\n",
       "      <td>37.000000</td>\n",
       "      <td>70000.000000</td>\n",
       "      <td>0.000000</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>75%</th>\n",
       "      <td>1.575036e+07</td>\n",
       "      <td>46.000000</td>\n",
       "      <td>88000.000000</td>\n",
       "      <td>1.000000</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>max</th>\n",
       "      <td>1.581524e+07</td>\n",
       "      <td>60.000000</td>\n",
       "      <td>150000.000000</td>\n",
       "      <td>1.000000</td>\n",
       "    </tr>\n",
       "  </tbody>\n",
       "</table>\n",
       "</div>"
      ],
      "text/plain": [
       "            User ID         Age  EstimatedSalary   Purchased\n",
       "count  4.000000e+02  400.000000       398.000000  400.000000\n",
       "mean   1.569154e+07   37.655000     69987.437186    0.357500\n",
       "std    7.165832e+04   10.482877     34005.146195    0.479864\n",
       "min    1.556669e+07   18.000000     15000.000000    0.000000\n",
       "25%    1.562676e+07   29.750000     43250.000000    0.000000\n",
       "50%    1.569434e+07   37.000000     70000.000000    0.000000\n",
       "75%    1.575036e+07   46.000000     88000.000000    1.000000\n",
       "max    1.581524e+07   60.000000    150000.000000    1.000000"
      ]
     },
     "execution_count": 2,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "df.describe()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "### Normal Distribution / Gaussian Distribution:\n",
    "- It is bell-curved in shape.\n",
    "- Data is symmetric and more data towards the mean and less data far from the mean. \n",
    "- Mean and median are equal.\n",
    "- It follows 68-95-99 where 68% of the data falls inside 1st std dev, 95% in 2nd std dev and 99% in 3rd std dev\n",
    "- Whatever data points outside of this 68-95-99 range are considered as outlier.\n",
    "\n",
    "![NormalDistribution](https://user-images.githubusercontent.com/8953894/58531965-a0f4ef80-81d3-11e9-8d3d-42b50dac49ec.png)"
   ]
  },
  {
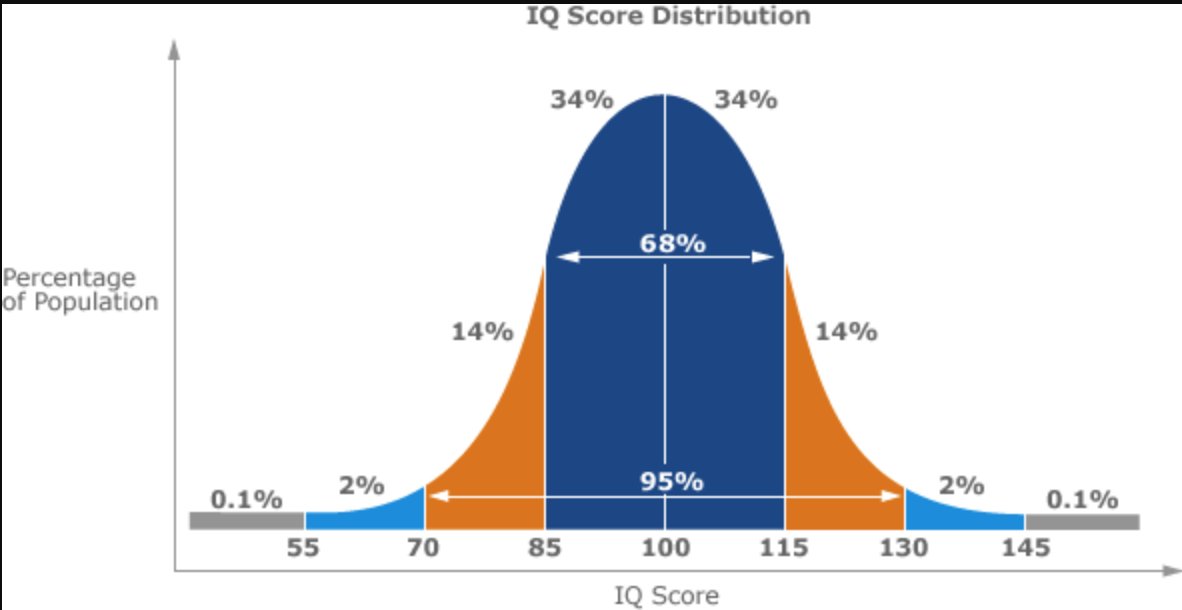   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "skip"
    }
   },
   "source": [
    "![68_95_99_rule](img/68_95_99_rule.svg)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "### Skewness\n",
    "    : It measures the balance of the data distribution.\n",
    "- Normal distribution has skew of 0(zero).\n",
    "\n",
    "**Positive skewness:** \n",
    "- It has +ve skewness where tail of the data is towards the right side of the distribution. \n",
    "- Outlier values are greater than the mean.\n",
    "\n",
    "**Negative skewness:** \n",
    "- It has -ve skewness where tail of the data is towards the left side of the distribution. \n",
    "- Outlier values are lesser than the mean.\n",
    "\n",
    "![Skewness](https://user-images.githubusercontent.com/8953894/58532014-cc77da00-81d3-11e9-99be-16055e86f2c8.png)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "###### Missing value Imputation:\n",
    "- A general approach to solve the problem of uncertainity and missing value in the data set.\n",
    "- Ex. A variable having numeric value, fill the missing value with mean or median.\n",
    "- A variable having categorical value, fill the missing value with mode."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 3,
   "metadata": {
    "slideshow": {
     "slide_type": "subslide"
    }
   },
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "\n",
      "Total missing values in Salary: \n",
      "EstimatedSalary      2\n",
      "Country            133\n",
      "dtype: int64\n",
      "\n",
      "Mean of 'Salary':  69987.43718592965\n",
      "\n",
      "Median of 'Salary':  70000.0\n",
      "\n",
      "Mode of 'Country':  UK\n",
      "\n",
      "After missing value imputation: \n"
     ]
    },
    {
     "data": {
      "text/html": [
       "<div>\n",
       "<style scoped>\n",
       "    .dataframe tbody tr th:only-of-type {\n",
       "        vertical-align: middle;\n",
       "    }\n",
       "\n",
       "    .dataframe tbody tr th {\n",
       "        vertical-align: top;\n",
       "    }\n",
       "\n",
       "    .dataframe thead th {\n",
       "        text-align: right;\n",
       "    }\n",
       "</style>\n",
       "<table border=\"1\" class=\"dataframe\">\n",
       "  <thead>\n",
       "    <tr style=\"text-align: right;\">\n",
       "      <th></th>\n",
       "      <th>User ID</th>\n",
       "      <th>Gender</th>\n",
       "      <th>Age</th>\n",
       "      <th>EstimatedSalary</th>\n",
       "      <th>Country</th>\n",
       "      <th>Purchased</th>\n",
       "    </tr>\n",
       "  </thead>\n",
       "  <tbody>\n",
       "    <tr>\n",
       "      <th>0</th>\n",
       "      <td>15624510</td>\n",
       "      <td>Male</td>\n",
       "      <td>19</td>\n",
       "      <td>19000.0</td>\n",
       "      <td>UK</td>\n",
       "      <td>0</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>1</th>\n",
       "      <td>15810944</td>\n",
       "      <td>Male</td>\n",
       "      <td>35</td>\n",
       "      <td>20000.0</td>\n",
       "      <td>UK</td>\n",
       "      <td>0</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>2</th>\n",
       "      <td>15668575</td>\n",
       "      <td>Female</td>\n",
       "      <td>26</td>\n",
       "      <td>43000.0</td>\n",
       "      <td>India</td>\n",
       "      <td>0</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>3</th>\n",
       "      <td>15603246</td>\n",
       "      <td>Female</td>\n",
       "      <td>27</td>\n",
       "      <td>57000.0</td>\n",
       "      <td>US</td>\n",
       "      <td>0</td>\n",
       "    </tr>\n",
       "    <tr>\n",
       "      <th>4</th>\n",
       "      <td>15804002</td>\n",
       "      <td>Male</td>\n",
       "      <td>19</td>\n",
       "      <td>76000.0</td>\n",
       "      <td>UK</td>\n",
       "      <td>0</td>\n",
       "    </tr>\n",
       "  </tbody>\n",
       "</table>\n",
       "</div>"
      ],
      "text/plain": [
       "    User ID  Gender  Age  EstimatedSalary Country  Purchased\n",
       "0  15624510    Male   19          19000.0      UK          0\n",
       "1  15810944    Male   35          20000.0      UK          0\n",
       "2  15668575  Female   26          43000.0   India          0\n",
       "3  15603246  Female   27          57000.0      US          0\n",
       "4  15804002    Male   19          76000.0      UK          0"
      ]
     },
     "execution_count": 3,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "null_columns = df.columns[df.isnull().any()]\n",
    "print('\\nTotal missing values in Salary: ')\n",
    "print(df[null_columns].isnull().sum())\n",
    "\n",
    "# Mean and Median\n",
    "mean = df['EstimatedSalary'].mean()\n",
    "median = df['EstimatedSalary'].median()\n",
    "print('\\nMean of \\'Salary\\': ', mean)\n",
    "print('\\nMedian of \\'Salary\\': ', median)\n",
    "df['EstimatedSalary'].fillna(median, inplace=True) # Fill NaN with median\n",
    "\n",
    "# Mode\n",
    "mode = df['Country'].mode()[0]\n",
    "print('\\nMode of \\'Country\\': ', mode)\n",
    "df['Country'].fillna(mode, inplace=True)  # Fill NaN with mode value.\n",
    "print('\\nAfter missing value imputation: ')\n",
    "df.head()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "slide"
    }
   },
   "source": [
    "## Data Visualization for variables"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "subslide"
    }
   },
   "source": [
    "**Univaraite Analysis:** Analysis on a one variable at a time.\n",
    "- For Categorical variable, visualization can be done using bar chart, pie chart.\n",
    "![Univariate](https://user-images.githubusercontent.com/8953894/58532089-f9c48800-81d3-11e9-865f-c3c309a251ac.png)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "subslide"
    }
   },
   "source": [
    "- For Numerical variable, visualization can be done using histogram, box-plot chart.\n",
    "    - Histogram: A histogram depicts the shape of the distribution by binning the values into discrete intervals.\n",
    "    ![Histogram](https://user-images.githubusercontent.com/8953894/58532118-0ba62b00-81d4-11e9-891d-65c8dc2a8d15.png)",
    "    "
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "subslide"
    }
   },
   "source": [
    "- Box-plot: A Box Plot represents quartile statistics. The box represents the IQR, and the median is a line cutting the box in half (or close to it). A box plot can also have whiskers, which typically represent the upper quartile boundary and lower quartile boundary and also known as a box and whiskers plot.\n",
    "    \n",
    "    ![Box](https://user-images.githubusercontent.com/8953894/58532155-25477280-81d4-11e9-9404-412c9b98f661.png)",
    "    "
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "subslide"
    }
   },
   "source": [
    "**Bivaraite Analysis:** Analysis on a two variables at a time.\n",
    "- Scatter plot: Visually represents the relationship between the 2 variables.\n",
    "    ![Scatter](https://user-images.githubusercontent.com/8953894/58532176-355f5200-81d4-11e9-83ab-cd4f28408eed.png)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "slideshow": {
     "slide_type": "subslide"
    }
   },
   "source": [
    "- Pair plot: It depicts the relationship between 2 varables by plotting all pairs of the variables.\n",
    "    ![Pair](https://user-images.githubusercontent.com/8953894/58532196-44460480-81d4-11e9-8910-0b1d63afad1b.png)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 17,
   "metadata": {
    "slideshow": {
     "slide_type": "subslide"
    }
   },
   "outputs": [
    {
     "data": {
      "text/plain": [
       "<matplotlib.axes._subplots.AxesSubplot at 0x7fe3d48adeb8>"
      ]
     },
     "execution_count": 17,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXoAAAD4CAYAAADiry33AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAC7hJREFUeJzt3H+o3fV9x/Hnq6btH7NQJXchjdmudBkj/rG0XJzQ/eEQ5o/+EfuP6B9tECH9Q6FC/1jaf9r9IThYWyhsQoquKXQ6oS2GVba50FHKsHojYo3OGdqICTG5XUvrKHQzvvdHvuIhu8k59557PMk7zwcc7vd8vt/vOe/A5enxe885qSokSX29b94DSJJmy9BLUnOGXpKaM/SS1Jyhl6TmDL0kNWfoJak5Qy9JzRl6SWpu07wHANi8eXMtLi7OewxJuqQcPnz451W1MO64iyL0i4uLLC8vz3sMSbqkJHltkuO8dCNJzRl6SWrO0EtSc4Zekpoz9JLUnKGXpOYMvSQ1Z+glqbmL4gNTl4rFfd+f9witHHvwk/MeQbos+Ipekpoz9JLU3NjQJ9me5AdJXkpyJMnnhvUvJzmR5PnhdtvIOV9IcjTJK0lunuU/QJJ0YZNco38L+HxVPZfkQ8DhJE8N+75WVX89enCSncCdwHXAR4B/TfKHVXVmIweXJE1m7Cv6qjpZVc8N228CLwPbLnDKbuCxqvptVf0MOApcvxHDSpLWbk3X6JMsAh8Dfjws3ZfkhSSPJLlqWNsGvD5y2nFW+Q9Dkr1JlpMsr6ysrHlwSdJkJg59kiuB7wD3V9WvgYeAjwK7gJPAV9byxFW1v6qWqmppYWHs9+ZLktZpotAneT9nI//tqvouQFWdqqozVfU28A3evTxzAtg+cvo1w5okaQ4meddNgIeBl6vqqyPrW0cO+xTw4rB9ELgzyQeTXAvsAJ7ZuJElSWsxybtuPgF8GvhJkueHtS8CdyXZBRRwDPgsQFUdSfI48BJn37Fzr++4kaT5GRv6qvoRkFV2PXmBcx4AHphiLknSBvGTsZLUnKGXpOYMvSQ1Z+glqTlDL0nNGXpJas7QS1Jzhl6SmjP0ktScoZek5gy9JDVn6CWpOUMvSc0ZeklqztBLUnOGXpKaM/SS1Jyhl6TmDL0kNWfoJak5Qy9JzRl6SWrO0EtSc4Zekpoz9JLUnKGXpOYMvSQ1Z+glqTlDL0nNGXpJas7QS1JzY0OfZHuSHyR5KcmRJJ8b1q9O8lSSV4efVw3rSfL1JEeTvJDk47P+R0iSzm+SV/RvAZ+vqp3ADcC9SXYC+4BDVbUDODTcB7gV2DHc9gIPbfjUkqSJjQ19VZ2squeG7TeBl4FtwG7gwHDYAeD2YXs38K0662ngw0m2bvjkkqSJrOkafZJF4GPAj4EtVXVy2PUGsGXY3ga8PnLa8WHt3Mfam2Q5yfLKysoax5YkTWri0Ce5EvgOcH9V/Xp0X1UVUGt54qraX1VLVbW0sLCwllMlSWswUeiTvJ+zkf92VX13WD71ziWZ4efpYf0EsH3k9GuGNUnSHEzyrpsADwMvV9VXR3YdBPYM23uAJ0bWPzO8++YG4Fcjl3gkSe+xTRMc8wng08BPkjw/rH0ReBB4PMk9wGvAHcO+J4HbgKPAb4C7N3RiSdKajA19Vf0IyHl237TK8QXcO+VckqQN4idjJak5Qy9JzRl6SWrO0EtSc4Zekpoz9JLUnKGXpOYMvSQ1Z+glqTlDL0nNGXpJas7QS1Jzhl6SmjP0ktScoZek5gy9JDVn6CWpOUMvSc0ZeklqztBLUnOGXpKaM/SS1Jyhl6TmDL0kNWfoJak5Qy9JzRl6SWrO0EtSc4Zekpoz9JLUnKGXpObGhj7JI0lOJ3lxZO3LSU4keX643Tay7wtJjiZ5JcnNsxpckjSZSV7RfxO4ZZX1r1XVruH2JECSncCdwHXDOX+b5IqNGlaStHZjQ19VPwR+MeHj7QYeq6rfVtXPgKPA9VPMJ0ma0jTX6O9L8sJwaeeqYW0b8PrIMceHNUnSnKw39A8BHwV2ASeBr6z1AZLsTbKcZHllZWWdY0iSxllX6KvqVFWdqaq3gW/w7uWZE8D2kUOvGdZWe4z9VbVUVUsLCwvrGUOSNIF1hT7J1pG7nwLeeUfOQeDOJB9Mci2wA3hmuhElSdPYNO6AJI8CNwKbkxwHvgTcmGQXUMAx4LMAVXUkyePAS8BbwL1VdWY2o0uSJjE29FV11yrLD1/g+AeAB6YZSpK0ccaGXtLFb3Hf9+c9QivHHvzkvEfYUH4FgiQ1Z+glqTlDL0nNGXpJas7QS1Jzhl6SmjP0ktScoZek5gy9JDVn6CWpOUMvSc0ZeklqztBLUnOGXpKaM/SS1Jyhl6TmDL0kNWfoJak5Qy9JzRl6SWrO0EtSc4Zekpoz9JLUnKGXpOYMvSQ1Z+glqTlDL0nNGXpJas7QS1Jzhl6SmjP0ktTc2NAneSTJ6SQvjqxdneSpJK8OP68a1pPk60mOJnkhycdnObwkabxJXtF/E7jlnLV9wKGq2gEcGu4D3ArsGG57gYc2ZkxJ0nqNDX1V/RD4xTnLu4EDw/YB4PaR9W/VWU8DH06ydaOGlSSt3Xqv0W+pqpPD9hvAlmF7G/D6yHHHh7X/J8neJMtJlldWVtY5hiRpnKn/GFtVBdQ6zttfVUtVtbSwsDDtGJKk81hv6E+9c0lm+Hl6WD8BbB857pphTZI0J+sN/UFgz7C9B3hiZP0zw7tvbgB+NXKJR5I0B5vGHZDkUeBGYHOS48CXgAeBx5PcA7wG3DEc/iRwG3AU+A1w9wxmliStwdjQV9Vd59l10yrHFnDvtENJkjaOn4yVpOYMvSQ1Z+glqTlDL0nNGXpJas7QS1Jzhl6SmjP0ktScoZek5gy9JDVn6CWpOUMvSc0ZeklqztBLUnOGXpKaM/SS1Jyhl6TmDL0kNWfoJak5Qy9JzRl6SWrO0EtSc4Zekpoz9JLUnKGXpOYMvSQ1Z+glqTlDL0nNGXpJas7QS1Jzhl6Smts0zclJjgFvAmeAt6pqKcnVwD8Ai8Ax4I6q+uV0Y0qS1msjXtH/WVXtqqql4f4+4FBV7QAODfclSXMyi0s3u4EDw/YB4PYZPIckaULThr6Af0lyOMneYW1LVZ0ctt8Atqx2YpK9SZaTLK+srEw5hiTpfKa6Rg/8aVWdSPK7wFNJ/mN0Z1VVklrtxKraD+wHWFpaWvUYSdL0pnpFX1Unhp+nge8B1wOnkmwFGH6ennZISdL6rTv0SX4nyYfe2Qb+HHgROAjsGQ7bAzwx7ZCSpPWb5tLNFuB7Sd55nL+vqn9K8izweJJ7gNeAO6YfU5K0XusOfVX9FPjjVdb/C7hpmqEkSRvHT8ZKUnOGXpKaM/SS1Jyhl6TmDL0kNWfoJak5Qy9JzRl6SWrO0EtSc4Zekpoz9JLUnKGXpOYMvSQ1Z+glqTlDL0nNGXpJas7QS1Jzhl6SmjP0ktScoZek5gy9JDVn6CWpOUMvSc0ZeklqztBLUnOGXpKaM/SS1Jyhl6TmDL0kNWfoJak5Qy9Jzc0s9EluSfJKkqNJ9s3qeSRJFzaT0Ce5Avgb4FZgJ3BXkp2zeC5J0oXN6hX99cDRqvppVf0P8Biwe0bPJUm6gE0zetxtwOsj948DfzJ6QJK9wN7h7n8neWVGs1yONgM/n/cQ4+Sv5j2B5sDfzY31+5McNKvQj1VV+4H983r+zpIsV9XSvOeQzuXv5nzM6tLNCWD7yP1rhjVJ0ntsVqF/FtiR5NokHwDuBA7O6LkkSRcwk0s3VfVWkvuAfwauAB6pqiOzeC6tyktiulj5uzkHqap5zyBJmiE/GStJzRl6SWrO0EtSc3N7H702TpI/4uwnj7cNSyeAg1X18vymknSx8BX9JS7JX3D2KyYCPDPcAjzql8lJAt91c8lL8p/AdVX1v+esfwA4UlU75jOZdH5J7q6qv5v3HJcLX9Ff+t4GPrLK+tZhn3Qx+st5D3A58Rr9pe9+4FCSV3n3i+R+D/gD4L65TaXLXpIXzrcL2PJeznK589JNA0nex9mvhh79Y+yzVXVmflPpcpfkFHAz8MtzdwH/XlWr/Z+oZsBX9A1U1dvA0/OeQzrHPwJXVtXz5+5I8m/v/TiXL1/RS1Jz/jFWkpoz9JLUnKGXpOYMvSQ1938BOI1SBEo+yQAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "# Bar Chart\n",
    "s = df['Purchased'].value_counts() ## Counts the occurrence of unqiue elements\n",
    "s.plot(kind='bar')"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 6,
   "metadata": {
    "slideshow": {
     "slide_type": "subslide"
    }
   },
   "outputs": [
    {
     "data": {
      "text/plain": [
       "<matplotlib.axes._subplots.AxesSubplot at 0x7fe3d48f3ba8>"
      ]
     },
     "execution_count": 6,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXQAAAD8CAYAAABn919SAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAE0FJREFUeJzt3W+MZfV93/H3J6yR8Y7L8se9Wi20S2WERb01NiNiCyuaARORYAUeIGSXRktEtU+ciNQbNZtIVZqqUYlU4vpB5XRlUvZB4oFQEAj/K9owSS01m+zauGtYIzBeYrawmz+7OEOR002/fTAHMyy7c++duXfu7G/fL2l07/l3z3e+mvuZM78559xUFZKks99PTLoASdJoGOiS1AgDXZIaYaBLUiMMdElqhIEuSY0w0CWpEQa6JDVioEBP8q+SPJPkO0m+lOTdSa5Isi/JC0keTHL+uIuVJJ1Z+l0pmmQL8A3g6qp6I8lDwFeAnwUeqaq5JL8LfLuqvrDca1166aW1devW0VQ+hNdff52NGzeu+X7PFvZnefanP3u0vNX258CBA39VVe/rt96GAV9vA3BBkv8LvAd4BbgB+Ofd8j3AvwWWDfStW7eyf//+AXc5OvPz88zMzKz5fs8W9md59qc/e7S81fYnyUuDrNd3yKWqjgD/EfgLFoP8NeAAcKKqTnarvQxsWVmpkqRR6HuEnuQi4FbgCuAE8IfAzYPuIMkOYAdAr9djfn5+RYWuxsLCwkT2e7awP8uzP/3Zo+WtVX8GGXL5BPD9qvpLgCSPANcDm5Js6I7SLwOOnG7jqtoN7AaYnp6uSfxZ5p+Dy7M/y7M//dmj5a1VfwY5y+UvgI8meU+SADcCzwJPAbd362wHHhtPiZKkQQwyhr4PeBj4JnCw22Y38KvAZ5O8AFwC3D/GOiVJfQx0lktV/QbwG6fMfhG4buQVSZJWxCtFJakRBrokNcJAl6RGDHqlqLQmtu768kT2e/jeWyayX2mUPEKXpEYY6JLUCANdkhphoEtSIwx0SWqEgS5JjTDQJakRBrokNcJAl6RGGOiS1AgDXZIaYaBLUiMMdElqhIEuSY3oG+hJrkry9JKvHyb55SQXJ3kyyfPd40VrUbAk6fQG+ZDo56rqmqq6BrgW+D/Ao8AuYG9VXQns7aYlSRMy7JDLjcD3quol4FZgTzd/D3DbKAuTJA1n2ED/FPCl7nmvql7pnr8K9EZWlSRpaKmqwVZMzgf+N/BPq+pokhNVtWnJ8uNV9Y5x9CQ7gB0AvV7v2rm5udFUPoSFhQWmpqbWfL9ni/XUn4NHXpvIfrdtufCMy9ZTf9Yre7S81fZndnb2QFVN91tvmM8U/Rngm1V1tJs+mmRzVb2SZDNw7HQbVdVuYDfA9PR0zczMDLHL0Zifn2cS+z1brKf+3DWpzxS9c+aMy9ZTf9Yre7S8terPMEMun+at4RaAx4Ht3fPtwGOjKkqSNLyBAj3JRuAm4JEls+8FbkryPPCJblqSNCEDDblU1evAJafM+2sWz3qRJK0DXikqSY0w0CWpEQa6JDXCQJekRhjoktQIA12SGmGgS1IjDHRJasQw93KRmrV1mXvI7Nx2cqz3mDl87y1je22dWzxCl6RGGOiS1AgDXZIaYaBLUiMMdElqhIEuSY0w0CWpEQa6JDXCQJekRgz6maKbkjyc5LtJDiX5WJKLkzyZ5Pnu8aJxFytJOrNBj9A/D3ytqj4AfAg4BOwC9lbVlcDeblqSNCF9Az3JhcBPAfcDVNXfVdUJ4FZgT7faHuC2cRUpSeovVbX8Csk1wG7gWRaPzg8A9wBHqmpTt06A429On7L9DmAHQK/Xu3Zubm6k38AgFhYWmJqaWvP9ni3WU38OHnlt0iW8Q+8COPrG+F5/25YLx/fia2Q9/QytR6vtz+zs7IGqmu633iCBPg38KXB9Ve1L8nngh8AvLQ3wJMeratlx9Onp6dq/f/9A38Aozc/PMzMzs+b7PVusp/4sd9fDSdm57ST3HRzfjUlbuNvievoZWo9W258kAwX6IGPoLwMvV9W+bvph4CPA0SSbu51tBo6ttFhJ0ur1DfSqehX4QZKrulk3sjj88jiwvZu3HXhsLBVKkgYy6N+RvwT8fpLzgReBX2Dxl8FDSe4GXgLuGE+JkqRBDBToVfU0cLrxmxtHW44kaaW8UlSSGmGgS1IjDHRJaoSBLkmNMNAlqREGuiQ1wkCXpEYY6JLUCANdkhphoEtSIwx0SWqEgS5JjTDQJakRBrokNcJAl6RGGOiS1AgDXZIaYaBLUiMG+gi6JIeBvwX+HjhZVdNJLgYeBLYCh4E7qur4eMqUJPUzzBH6bFVdU1VvfrboLmBvVV0J7O2mJUkTspohl1uBPd3zPcBtqy9HkrRSqar+KyXfB44DBfyXqtqd5ERVbeqWBzj+5vQp2+4AdgD0er1r5+bmRln/QBYWFpiamlrz/Z4t1lN/Dh55bdIlvEPvAjj6xvhef9uWC8f34mtkPf0MrUer7c/s7OyBJaMjZzTQGDrw8ao6kuQfAk8m+e7ShVVVSU77m6GqdgO7Aaanp2tmZmbAXY7O/Pw8k9jv2WI99eeuXV+edAnvsHPbSe47OOhbZXiH75wZ22uvlfX0M7QerVV/Bhpyqaoj3eMx4FHgOuBoks0A3eOxcRUpSeqvb6An2ZjkvW8+B34a+A7wOLC9W2078Ni4ipQk9TfI35E94NHFYXI2AH9QVV9L8ufAQ0nuBl4C7hhfmZKkfvoGelW9CHzoNPP/GrhxHEVJkobnlaKS1AgDXZIaYaBLUiMMdElqhIEuSY0Y3+VvWrWta3TV5M5tJ992hebhe29Zk/1KGi2P0CWpEQa6JDXCQJekRhjoktQIA12SGmGgS1IjDHRJaoSBLkmNMNAlqREGuiQ1wkCXpEYY6JLUiIEDPcl5Sb6V5Ilu+ook+5K8kOTBJOePr0xJUj/DHKHfAxxaMv3bwOeq6v3AceDuURYmSRrOQIGe5DLgFuCL3XSAG4CHu1X2ALeNo0BJ0mBSVf1XSh4G/gPwXuBXgLuAP+2OzklyOfDVqvrgabbdAewA6PV6187NzY2s+EEtLCwwNTW15vtdrYNHXluT/fQugKNvvDW9bcuFa7Lf01mr73kYp/Zn1CbZ71E5W99ja2W1/ZmdnT1QVdP91uv7ARdJPgkcq6oDSWaGLaSqdgO7Aaanp2tmZuiXWLX5+Xkmsd/VumsNP+DivoNv/SgcvnNmTfZ7Omv1PQ/j1P6M2iT7PSpn63tsraxVfwb5Kb0e+LkkPwu8G/gHwOeBTUk2VNVJ4DLgyPjKlCT103cMvap+raouq6qtwKeAP6qqO4GngNu71bYDj42tSklSX6s5D/1Xgc8meQG4BLh/NCVJklZiqIHBqpoH5rvnLwLXjb4kSdJKeKWoJDXCQJekRozvXKxGbF2Hp9FJ0ul4hC5JjTDQJakRBrokNcJAl6RGGOiS1AjPctE7eGbP2ppUvw/fe8tE9qvx8QhdkhphoEtSIwx0SWqEgS5JjTDQJakRBrokNcJAl6RGGOiS1Ii+gZ7k3Un+LMm3kzyT5De7+Vck2ZfkhSQPJjl//OVKks5kkCtFfwTcUFULSd4FfCPJV4HPAp+rqrkkvwvcDXxhjLVKGqFRXqG6c9tJ7hri9bxKdTz6HqHXooVu8l3dVwE3AA938/cAt42lQknSQAYaQ09yXpKngWPAk8D3gBNVdbJb5WVgy3hKlCQNIlU1+MrJJuBR4N8AD1TV+7v5lwNfraoPnmabHcAOgF6vd+3c3Nwo6h7KwsICU1NTK9r24JHXRlzN+tO7AI6+Mekq1i/709+wPdq25cLxFbMOrSaDAGZnZw9U1XS/9Ya622JVnUjyFPAxYFOSDd1R+mXAkTNssxvYDTA9PV0zMzPD7HIk5ufnWel+hxkXPFvt3HaS+w56480zsT/9Ddujw3fOjK+YdWg1GTSMQc5yeV93ZE6SC4CbgEPAU8Dt3WrbgcfGVaQkqb9BfqVuBvYkOY/FXwAPVdUTSZ4F5pL8e+BbwP1jrFOS1EffQK+q/wV8+DTzXwSuG0dRkqThnTUDg6s5Z3bYc2QltWlSnw71wM0b12Q/XvovSY0w0CWpEQa6JDXCQJekRhjoktQIA12SGmGgS1IjDHRJaoSBLkmNMNAlqREGuiQ1wkCXpEYY6JLUCANdkhphoEtSIwx0SWqEgS5JjRjkQ6IvT/JUkmeTPJPknm7+xUmeTPJ893jR+MuVJJ3JIEfoJ4GdVXU18FHgM0muBnYBe6vqSmBvNy1JmpC+gV5Vr1TVN7vnfwscArYAtwJ7utX2ALeNq0hJUn9DjaEn2Qp8GNgH9KrqlW7Rq0BvpJVJkoaSqhpsxWQK+GPgt6rqkSQnqmrTkuXHq+od4+hJdgA7AHq93rVzc3MrKvTgkddWtB1A7wI4+saKN2+e/Vme/elv2B5t23Lh+IpZxmpyZDWuuPA8pqamVrz97Ozsgaqa7rfeQIGe5F3AE8DXq+p3unnPATNV9UqSzcB8VV213OtMT0/X/v37B/oGTrV115dXtB3Azm0nue/ghhVv3zr7szz709+wPTp87y1jrObMVpMjq/HAzRuZmZlZ8fZJBgr0Qc5yCXA/cOjNMO88Dmzvnm8HHltJoZKk0RjkV+r1wM8DB5M83c37deBe4KEkdwMvAXeMp0RJ0iD6BnpVfQPIGRbfONpyJEkr5cCgpDU3qbHs1nnpvyQ1wkCXpEYY6JLUCANdkhphoEtSIwx0SWqEgS5JjTDQJakRBrokNcJAl6RGGOiS1AgDXZIaYaBLUiMMdElqhIEuSY0w0CWpEQa6JDVikA+J/r0kx5J8Z8m8i5M8meT57vGi8ZYpSepnkCP0B4CbT5m3C9hbVVcCe7tpSdIE9Q30qvoT4G9OmX0rsKd7vge4bcR1SZKGtNIx9F5VvdI9fxXojageSdIKpar6r5RsBZ6oqg920yeqatOS5cer6rTj6El2ADsAer3etXNzcysq9OCR11a0HUDvAjj6xoo3b579WZ796c8eLe+KC89jampqxdvPzs4eqKrpfuttWOHrH02yuapeSbIZOHamFatqN7AbYHp6umZmZla0w7t2fXlF2wHs3HaS+w6u9Fttn/1Znv3pzx4t74GbN7LS7BvGSodcHge2d8+3A4+NphxJ0koNctril4D/CVyV5OUkdwP3AjcleR74RDctSZqgvn8jVdWnz7DoxhHXIklaBa8UlaRGGOiS1AgDXZIaYaBLUiMMdElqhIEuSY0w0CWpEQa6JDXCQJekRhjoktQIA12SGmGgS1IjDHRJaoSBLkmNMNAlqREGuiQ1wkCXpEYY6JLUiFUFepKbkzyX5IUku0ZVlCRpeCsO9CTnAf8Z+BngauDTSa4eVWGSpOGs5gj9OuCFqnqxqv4OmANuHU1ZkqRhrSbQtwA/WDL9cjdPkjQBqaqVbZjcDtxcVf+ym/554Cer6hdPWW8HsKObvAp4buXlrtilwF9NYL9nC/uzPPvTnz1a3mr784+r6n39Vtqwih0cAS5fMn1ZN+9tqmo3sHsV+1m1JPuranqSNaxn9md59qc/e7S8terPaoZc/hy4MskVSc4HPgU8PpqyJEnDWvERelWdTPKLwNeB84Dfq6pnRlaZJGkoqxlyoaq+AnxlRLWM00SHfM4C9md59qc/e7S8NenPiv8pKklaX7z0X5Ia0VSgJ7k8yVNJnk3yTJJ7uvkXJ3kyyfPd40WTrnUSkrw7yZ8l+XbXn9/s5l+RZF93C4cHu39yn9OSnJfkW0me6KbtUSfJ4SQHkzydZH83z/fYEkk2JXk4yXeTHErysbXoUVOBDpwEdlbV1cBHgc90tyPYBeytqiuBvd30uehHwA1V9SHgGuDmJB8Ffhv4XFW9HzgO3D3BGteLe4BDS6bt0dvNVtU1S07F8z32dp8HvlZVHwA+xOLP0vh7VFXNfgGPATexeDHT5m7eZuC5Sdc26S/gPcA3gZ9k8YKHDd38jwFfn3R9E+7NZd0b7gbgCSD26G39OQxceso832Nv9eJC4Pt0/6Ncyx61doT+Y0m2Ah8G9gG9qnqlW/Qq0JtQWRPXDSU8DRwDngS+B5yoqpPdKt7CAf4T8K+B/9dNX4I9WqqA/57kQHclOPgeW+oK4C+B/9oN230xyUbWoEdNBnqSKeC/Ab9cVT9cuqwWfz2es6f2VNXfV9U1LB6FXgd8YMIlrStJPgkcq6oDk65lHft4VX2ExTutfibJTy1deK6/x1g8HfwjwBeq6sPA65wyvDKuHjUX6EnexWKY/35VPdLNPppkc7d8M4tHp+e0qjoBPMXi8MGmJG9ek3DaWzicQ64Hfi7JYRbvIHoDi+Oh9qhTVUe6x2PAoyweGPgee8vLwMtVta+bfpjFgB97j5oK9CQB7gcOVdXvLFn0OLC9e76dxbH1c06S9yXZ1D2/gMX/LxxiMdhv71Y7Z/sDUFW/VlWXVdVWFm9n8UdVdSf2CIAkG5O8983nwE8D38H32I9V1avAD5Jc1c26EXiWNehRUxcWJfk48D+Ag7w1/vnrLI6jPwT8I+Al4I6q+puJFDlBSf4ZsIfFWzX8BPBQVf27JP+ExaPRi4FvAf+iqn40uUrXhyQzwK9U1Sft0aKuD492kxuAP6iq30pyCb7HfizJNcAXgfOBF4FfoHvPMcYeNRXoknQua2rIRZLOZQa6JDXCQJekRhjoktQIA12SGmGgS1IjDHRJaoSBLkmN+P+eR7Pqhu7suQAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "# Histogram\n",
    "df['Age'].hist()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 7,
   "metadata": {
    "slideshow": {
     "slide_type": "subslide"
    }
   },
   "outputs": [
    {
     "data": {
      "text/plain": [
       "<matplotlib.axes._subplots.AxesSubplot at 0x7fe3d48b3390>"
      ]
     },
     "execution_count": 7,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAY0AAAD8CAYAAACLrvgBAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAFkpJREFUeJzt3X+wX3Wd3/Hnq0QUf0BA9A6TMIbRjBVp3cIdoHXG3ooNQa1hpmih7hJdxnQL7q/ursbdzmYXly7WnVLpKDNZSQkOI1J2XVISyWaQW2dbg6AoP3W54g+S4YcSQBF/hX33j+8n63fDTe4n95ubS8LzMXPmnvM+n885n+/Md+7rns853+9NVSFJUo9/NN8DkCQdPAwNSVI3Q0OS1M3QkCR1MzQkSd0MDUlSN0NDktTN0JAkdTM0JEndFsz3APa3Y489tpYsWTLfw5Ce5Uc/+hEveclL5nsY0rS+/OUvf7+qXjFTu0MuNJYsWcLtt98+38OQnmVycpKJiYn5HoY0rSTf6Wnn9JQkqZuhIUnqZmhIkroZGpKkboaGJKmboSFJ6mZoSJK6GRqSpG6H3If7pAMlyQE5T1UdkPNIPbzSkGapqvZpedUHb9znPgaGnmsMDUlSN0NDktTN0JAkdTM0JEndDA1JUjdDQ5LUzdCQJHUzNCRJ3QwNSVK3GUMjybokjya5e5p9v5OkkhzbtpPk8iRTSe5McvJQ25VJ7m/LyqH6KUnuan0uT/tuhiTHJNnS2m9JcvT+ecmSpNnqudK4Cli+ezHJ8cAy4LtD5bOApW1ZBVzR2h4DrAFOA04F1gyFwBXA+4b67TrXauDmqloK3Ny2JUnzaMbQqKovADum2XUZ8AFg+MtxVgBX18BWYGGS44AzgS1VtaOqHge2AMvbviOramsNvmTnauDsoWOtb+vrh+qSpHkyq3saSVYA26vqa7vtWgQ8OLS9rdX2Vt82TR1grKoeausPA2OzGaskaf/Z569GT/Ji4PcZTE0dEFVVSfb4dZ9JVjGYDmNsbIzJyckDNTRpn/je1MFuNv9P49XACcDX2j3rxcBXkpwKbAeOH2q7uNW2AxO71SdbffE07QEeSXJcVT3UprEe3dOAqmotsBZgfHy8JiYm9tRUmj83bcT3pg52+zw9VVV3VdUrq2pJVS1hMKV0clU9DGwAzm9PUZ0OPNmmmDYDy5Ic3W6ALwM2t30/SHJ6e2rqfOCGdqoNwK6nrFYO1SVJ86TnkdtPA18EXptkW5IL9tJ8E/AAMAX8OXAhQFXtAD4M3NaWi1uN1uaTrc83gc+1+qXAv05yP/CWti1JmkczTk9V1Xkz7F8ytF7ARXtotw5YN039duCkaeqPAWfMND5J0oHjJ8IlSd0MDUlSN0NDktTN0JAkdTM0JEndDA1JUjdDQ5LUzdCQJHUzNCRJ3QwNSVI3Q0OS1M3QkCR1MzQkSd0MDUlSN0NDktTN0JAkdTM0JEndDA1JUjdDQ5LUzdCQJHUzNCRJ3WYMjSTrkjya5O6h2keTfD3JnUk+m2Th0L4PJZlK8o0kZw7Vl7faVJLVQ/UTktza6p9Jcnirv7BtT7X9S/bXi5YkzU7PlcZVwPLdaluAk6rqnwJ/C3wIIMmJwLnA61ufTyQ5LMlhwMeBs4ATgfNaW4CPAJdV1WuAx4ELWv0C4PFWv6y1kyTNoxlDo6q+AOzYrfbXVbWzbW4FFrf1FcC1VfXTqvoWMAWc2papqnqgqn4GXAusSBLgzcD1rf964OyhY61v69cDZ7T2kqR5smA/HONXgc+09UUMQmSXba0G8OBu9dOAlwNPDAXQcPtFu/pU1c4kT7b23999AElWAasAxsbGmJycHO0VSXPE96YOdiOFRpI/AHYC1+yf4cxOVa0F1gKMj4/XxMTEfA5Hmt5NG/G9qYPdrEMjyXuAtwNnVFW18nbg+KFmi1uNPdQfAxYmWdCuNobb7zrWtiQLgKNae0nSPJnVI7dJlgMfAN5RVU8P7doAnNuefDoBWAp8CbgNWNqelDqcwc3yDS1sbgHOaf1XAjcMHWtlWz8H+PxQOEmS5sGMVxpJPg1MAMcm2QasYfC01AuBLe3e9Naq+rWquifJdcC9DKatLqqqZ9px3g9sBg4D1lXVPe0UHwSuTfInwB3Ala1+JfCpJFMMbsSfux9eryRpBDOGRlWdN035ymlqu9pfAlwyTX0TsGma+gMMnq7avf4T4J0zjU+SdOD4iXBJUjdDQ5LUzdCQJHUzNCRJ3QwNSVI3Q0OS1M3QkCR1MzQkSd0MDUlSN0NDktTN0JAkdTM0JEndDA1JUjdDQ5LUzdCQJHUzNCRJ3QwNSVI3Q0OS1M3QkCR1MzQkSd1mDI0k65I8muTuodoxSbYkub/9PLrVk+TyJFNJ7kxy8lCfla39/UlWDtVPSXJX63N5kuztHJKk+dNzpXEVsHy32mrg5qpaCtzctgHOApa2ZRVwBQwCAFgDnAacCqwZCoErgPcN9Vs+wzkkSfNkxtCoqi8AO3YrrwDWt/X1wNlD9atrYCuwMMlxwJnAlqraUVWPA1uA5W3fkVW1taoKuHq3Y013DknSPFkwy35jVfVQW38YGGvri4AHh9pta7W91bdNU9/bOZ4lySoGVzaMjY0xOTm5jy9HOjB8b+pgN9vQ+HtVVUlqfwxmtueoqrXAWoDx8fGamJiYy+FIs3PTRnxv6mA326enHmlTS7Sfj7b6duD4oXaLW21v9cXT1Pd2DknSPJltaGwAdj0BtRK4Yah+fnuK6nTgyTbFtBlYluTodgN8GbC57ftBktPbU1Pn73as6c4hSZonM05PJfk0MAEcm2Qbg6egLgWuS3IB8B3gXa35JuCtwBTwNPBegKrakeTDwG2t3cVVtevm+oUMntA6AvhcW9jLOSRJ82TG0Kiq8/aw64xp2hZw0R6Osw5YN039duCkaeqPTXcOSdL88RPhkqRuhoYkqZuhIUnqZmhIkroZGpKkboaGJKmboSFJ6mZoSJK6GRqSpG6GhiSpm6EhSepmaEiSuo38T5ikQ8Eb/vivefLHP5/z8yxZvXFOj3/UES/ga2uWzek59PxmaEjAkz/+Od++9G1zeo7Jyck5/899cx1KktNTkqRuhoYkqZuhIUnqZmhIkroZGpKkboaGJKnbSKGR5LeT3JPk7iSfTvKiJCckuTXJVJLPJDm8tX1h255q+5cMHedDrf6NJGcO1Ze32lSS1aOMVZI0ulmHRpJFwG8A41V1EnAYcC7wEeCyqnoN8DhwQetyAfB4q1/W2pHkxNbv9cBy4BNJDktyGPBx4CzgROC81laSNE9GnZ5aAByRZAHwYuAh4M3A9W3/euDstr6ibdP2n5EkrX5tVf20qr4FTAGntmWqqh6oqp8B17a2kqR5MuvQqKrtwJ8B32UQFk8CXwaeqKqdrdk2YFFbXwQ82PrubO1fPlzfrc+e6pKkeTLrrxFJcjSDv/xPAJ4A/heD6aUDLskqYBXA2NgYk5OT8zEMHeTm+n3z1FNPHZD3pu9/zaVRvnvqLcC3qup7AEn+EngjsDDJgnY1sRjY3tpvB44HtrXprKOAx4bquwz32VP9H6iqtcBagPHx8Zrr7/fRIeimjXP+vVAH4runDsTr0PPbKPc0vgucnuTF7d7EGcC9wC3AOa3NSuCGtr6hbdP2f76qqtXPbU9XnQAsBb4E3AYsbU9jHc7gZvmGEcYrSRrRrK80qurWJNcDXwF2Ancw+Gt/I3Btkj9ptStblyuBTyWZAnYwCAGq6p4k1zEInJ3ARVX1DECS9wObGTyZta6q7pnteCVJoxvpq9Grag2wZrfyAwyefNq97U+Ad+7hOJcAl0xT3wRsGmWMkqT9x0+ES5K6GRqSpG6GhiSpm6EhSepmaEiSuhkakqRuhoYkqZuhIUnqZmhIkrqN9Ilw6VDxstet5p+sPwD/HHL9zE1G8bLXAbxtbk+i5zVDQwJ+eN+lfPvSuf1leyC+5XbJ6o1zenzJ6SlJUjdDQ5LUzdCQJHUzNCRJ3QwNSVI3Q0OS1M3QkCR1MzQkSd0MDUlSt5FCI8nCJNcn+XqS+5L88yTHJNmS5P728+jWNkkuTzKV5M4kJw8dZ2Vrf3+SlUP1U5Lc1fpcniSjjFeSNJpRrzQ+BtxUVf8YeANwH7AauLmqlgI3t22As4ClbVkFXAGQ5BhgDXAacCqwZlfQtDbvG+q3fMTxSpJGMOvQSHIU8CbgSoCq+llVPQGs4Bdfy7YeOLutrwCuroGtwMIkxwFnAluqakdVPQ5sAZa3fUdW1daqKuDqoWNJkubBKFcaJwDfA/5nkjuSfDLJS4CxqnqotXkYGGvri4AHh/pva7W91bdNU5ckzZNRvuV2AXAy8OtVdWuSj/GLqSgAqqqS1CgD7JFkFYMpL8bGxpicnJzrU+oQNNfvm6eeeuqAvDd9/2sujRIa24BtVXVr276eQWg8kuS4qnqoTTE92vZvB44f6r+41bYDE7vVJ1t98TTtn6Wq1gJrAcbHx2uuv35ah6CbNs7515YfiK9GPxCvQ89vs56eqqqHgQeTvLaVzgDuBTYAu56AWgnc0NY3AOe3p6hOB55s01ibgWVJjm43wJcBm9u+HyQ5vT01df7QsSRJ82DUf8L068A1SQ4HHgDeyyCIrktyAfAd4F2t7SbgrcAU8HRrS1XtSPJh4LbW7uKq2tHWLwSuAo4APtcWSdI8GSk0quqrwPg0u86Ypm0BF+3hOOuAddPUbwdOGmWMkqT9x0+ES5K6GRqSpG6GhiSpm6EhSepmaEiSuhkakqRuhoYkqZuhIUnqZmhIkroZGpKkboaGJKmboSFJ6mZoSJK6GRqSpG6GhiSpm6EhSepmaEiSuhkakqRuhoYkqdtI/yNcOpQsWb1x7k9y09ye46gjXjCnx5cMDQn49qVvm/NzLFm98YCcR5pLI09PJTksyR1JbmzbJyS5NclUks8kObzVX9i2p9r+JUPH+FCrfyPJmUP15a02lWT1qGOVJI1mf9zT+E3gvqHtjwCXVdVrgMeBC1r9AuDxVr+stSPJicC5wOuB5cAnWhAdBnwcOAs4ETivtZUkzZORQiPJYuBtwCfbdoA3A9e3JuuBs9v6irZN239Ga78CuLaqflpV3wKmgFPbMlVVD1TVz4BrW1tJ0jwZ9Z7Gfwc+ALysbb8ceKKqdrbtbcCitr4IeBCgqnYmebK1XwRsHTrmcJ8Hd6ufNt0gkqwCVgGMjY0xOTk5+1ckzSHfmzrYzTo0krwdeLSqvpxkYv8Nad9V1VpgLcD4+HhNTMzrcKTp3bQR35s62I1ypfFG4B1J3gq8CDgS+BiwMMmCdrWxGNje2m8Hjge2JVkAHAU8NlTfZbjPnuqSpHkw63saVfWhqlpcVUsY3Mj+fFW9G7gFOKc1Wwnc0NY3tG3a/s9XVbX6ue3pqhOApcCXgNuApe1prMPbOTbMdrySpNHNxec0Pghcm+RPgDuAK1v9SuBTSaaAHQxCgKq6J8l1wL3ATuCiqnoGIMn7gc3AYcC6qrpnDsYrSeq0X0KjqiaBybb+AIMnn3Zv8xPgnXvofwlwyTT1TcCm/TFGSdLo/O4pSVI3Q0OS1M3QkCR1MzQkSd0MDUlSN0NDktTN0JAkdTM0JEndDA1JUjdDQ5LUzdCQJHUzNCRJ3QwNSVI3Q0OS1M3QkCR1MzQkSd0MDUlSN0NDktTN0JAkdTM0JEndZh0aSY5PckuSe5Pck+Q3W/2YJFuS3N9+Ht3qSXJ5kqkkdyY5eehYK1v7+5OsHKqfkuSu1ufyJBnlxUqSRjPKlcZO4Heq6kTgdOCiJCcCq4Gbq2opcHPbBjgLWNqWVcAVMAgZYA1wGnAqsGZX0LQ27xvqt3yE8UqSRjTr0Kiqh6rqK239h8B9wCJgBbC+NVsPnN3WVwBX18BWYGGS44AzgS1VtaOqHge2AMvbviOramtVFXD10LEkSfNgv9zTSLIE+GfArcBYVT3Udj0MjLX1RcCDQ922tdre6tumqUuS5smCUQ+Q5KXAXwC/VVU/GL7tUFWVpEY9R8cYVjGY8mJsbIzJycm5PqU0K743dbAbKTSSvIBBYFxTVX/Zyo8kOa6qHmpTTI+2+nbg+KHui1ttOzCxW32y1RdP0/5ZqmotsBZgfHy8JiYmpmsmza+bNuJ7Uwe7UZ6eCnAlcF9V/behXRuAXU9ArQRuGKqf356iOh14sk1jbQaWJTm63QBfBmxu+36Q5PR2rvOHjiVJmgejXGm8EfgV4K4kX2213wcuBa5LcgHwHeBdbd8m4K3AFPA08F6AqtqR5MPAba3dxVW1o61fCFwFHAF8ri2SpHky69Coqr8B9vS5iTOmaV/ARXs41jpg3TT124GTZjtGSdL+5SfCJUndDA1JUreRH7mVnq9m8602+ci+n2cwsys9N3ilIc1SVe3Tcsstt+xzHwNDzzWGhiSpm6EhSepmaEiSuhkakqRuhoYkqZuhIUnqZmhIkroZGpKkbjnUPjyU5HsMvl1Xeq45Fvj+fA9C2oNXVdUrZmp0yIWG9FyV5PaqGp/vcUijcHpKktTN0JAkdTM0pANn7XwPQBqV9zQkSd280pAkdTM0dMhI8kySrw4tq/fS9uwkJw5tX5zkLfthDAuTXDiLfn+U5Hfb+ulJbm2v4b4kfzRD34kkN85yyNI+8T/36VDy46r6pc62ZwM3AvcCVNUf7qcxLAQuBD4xwjHWA++qqq8lOQx47X4ZWZNkQVXt3J/H1POHVxo65CW5NMm9Se5M8mdJ/gXwDuCj7a/5Vye5Ksk5rf23k/xp23d7kpOTbE7yzSS/1tq8NMnNSb6S5K4kK9rpLgVe3fp+tLX9vSS3tfP/8dC4/iDJ3yb5G/5hMLwSeAigqp6pqntb+1OTfDHJHUn+X5Jnhcme2iR5T5INST4P3Jzk6iRnD/W7Zug1SHs2m38/6eLyXFyAZ4CvDi3/Dng58A1+8dDHwvbzKuCcob5/vw18G/iPbf0y4E7gZcArgEdafQFwZFs/FpgCAiwB7h467jIGT02FwR9pNwJvAk4B7gJeDBzZ+v9u6/OHwOPAZ4H/ALyo1Y8EFrT1twB/0dYngBtnaPMeYBtwTNv+l8BftfWjgG/t6ufisrfF6SkdSp41PZVkAfAT4Mo2798797+h/bwLeGlV/RD4YZKfJlkI/Aj4L0neBPwdsAgYm+Y4y9pyR9t+KbCUQQh9tqqebuPcdT6q6uIk17R+/x44j0EwHAWsT7IUKOAF05xvb222VNWOdo7/k+QTSV4B/FsG4eKUlWbk9JQOae0X4anA9cDbgZs6u/60/fy7ofVd2wuAdzO48jilBdUjwIumOU6AP62qX2rLa6rqyo5xf7OqrgDOAN6Q5OXAh4Fbquok4N/s4Xx7a/Oj3dpeDfwy8F5g3UxjksDQ0CEuyUuBo6pqE/DbwBvarh8y+Gt/to4CHq2qnyf5V8Cr9nDczcCvtnGQZFGSVwJfAM5OckSSlzH4Bb9rzG9Lkra5lMG02xPtnNtb/T17GddMbXa5CvgtgGr3TaSZOD2lQ8kRSb46tH0T8DHghiQvYvBX/39q+64F/jzJbwDnzOJc1wD/O8ldwO3A1wGq6rEk/zfJ3cDnqur3krwO+GLLgaeAX66qryT5DPA14FHgtqFj/wpwWZKngZ3Au6vqmST/lcHU038GNu5hXD1taGN9JMl9wF/N4vXrecpPhEvPU0lezOCezclV9eR8j0cHB6enpOeh9kHG+4D/YWBoX3ilIUnq5pWGJKmboSFJ6mZoSJK6GRqSpG6GhiSpm6EhSer2/wFBiwwKwRSlewAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "# Box Plot\n",
    "df[['EstimatedSalary']].boxplot()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 8,
   "metadata": {
    "slideshow": {
     "slide_type": "subslide"
    }
   },
   "outputs": [
    {
     "data": {
      "text/plain": [
       "<matplotlib.axes._subplots.AxesSubplot at 0x7fe3d48a3908>"
      ]
     },
     "execution_count": 8,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAZsAAAEKCAYAAADEovgeAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJztvXuUXNV1oP/tfqglkIREQzRILVmyhe3Fw5JNx6AQEwI2xg5BdqIokBAxHhxmjV8kgBF4fgvHOM4YO2MG4sQzDGCj4BgLERt5BkxkHsEwvFqOBBa2Q5uXWoCA1gNJSC119/79cW+1qlp1H31vnbqnqva3VktV577OPXXP3efssx+iqhiGYRiGS9qKroBhGIbR/JiwMQzDMJxjwsYwDMNwjgkbwzAMwzkmbAzDMAznmLAxDMMwnGPCxjAMw3COCRvDMAzDOSZsDMMwDOd0FF0BXzjqqKN0/vz5RVfDMAyjoVi/fv0bqnp00n4mbELmz59PX19f0dUwDMNoKETkxTT7mRrNMAzDcI4JG8MwDMM5JmwMwzAM55iwMQzDMJxjwsYwDMNwjgkboykZ3D3Exs07GNw9VHRVjAbFnqHaYqbPRtNx14YtrLzzKTrb2jgwOsrX/vA9nLt4TtHVMhoIe4Zqj81sjKZicPcQK+98in0HRtk1NMy+A6NccedTFaNTG7FaG8SR5hkyJo7NbIxCGdw9xMD2vfTMnEL31K7c5xvYvpfOtjb2MTpW1tnWxsD2vXRP7bIRKzZqTyLpGTKyYcLGKAwXL72emVM4MDpaUXZgdJSemVMqRqylF8kVdz7FqQuPapmXiLVBMnHPkJEdU6MZheBKVdE9tYuv/eF7mNzZxrSuDiZ3tvG1P3wP3VO7xkas5ZRGrGnr3Oiqp7xt0ArEPUNGdmxmYxSCS1XFuYvncOrCow5Rz+UZseadhdVaXZgVG7UfJO43iXqGjOyYsDEKwfVLr3tq1yEviNKI9YpxQiPpRZJX9eTTGknWNmg20vwm1Z4hIzsmbIxCKOqll2XEmmcW5uMaSauP2n38TVoBEzZGYRT10pvoiDXtLKyaWsZXyybfRu31VDP6+pvkwRc1bRwmbIxC8e2lV400s7AotUzPzCnsGx6pON++4ZGWXCOJot5qxlqocH16uSe1ny91NWFjGCmIm4XFqWUAVLXiXOO/tzJFqLTyqnB9WoNLaj+f6mrCxjBSEjULi1PLAEzp7GDX0PDYtimdHTVT2fgyas1KUSqtrCpc39Z7kp49n+pqwsYwcpKklnFldefTqDUredbD0myLI4sK17f1nrj2862uzpw6ReQWEXlNRH5eZdtlIqIiclT4XUTkBhHpF5GnROR9ZfteKCLPhn8XlpWfJCJPh8fcICISlh8pIuvC/deJyExX92gYEO8E6MpBsFnid6Vpn7s2bOHUa+/ngpse59Rr72fthi2ptrnANz+luPbzra7iSn8sIqcBu4FVqnpCWflc4Cbg3cBJqvqGiHwU+CzwUeBk4HpVPVlEjgT6gF5AgfXhMdtF5Angc8DjwN3ADap6j4h8Ddimql8VkSuBmaq6Mqm+vb292tfXV7sGMFoOF6PvKDZu3sEFNz1eoZ6b1tXBbZ88mUVzZ+Q+f72Jap/B3UOceu397Dtw8KU5ubONR1aeARC5zeXIfe2GLYes9xQ9o4xqv3rUVUTWq2pv0n7O1Giq+pCIzK+y6TrgCuCusrKlBEJJgcdEZIaIHAOcDqxT1W0AIrIOOFtEHgSmq+pjYfkq4GPAPeG5Tg/PeyvwIJAobAwjL3FqmVpb3RU5anWxTpR1PayR1ntcEtV+PtW1rms2IrIU2KKqG0OtV4k5wOay7wNhWVz5QJVygFmq+kr4+VVgVs1uwDA8oSinWN/MlIsSuI1gsl/Cl7rWTdiIyGHAF4Cz6nVNVVURidQTisjFwMUA8+bNq1e1DKMm1HvUWqSZ8ufXbKRd2hjRSqHqUuA2uqWfb9RzZvMOYAFQmtX0AD8TkfcDW4C5Zfv2hGVbOKgSK5U/GJb3VNkfYKuIHKOqr4SquNeiKqSqNwI3QrBmk/XGWh3rlMm4aqN6jlqLsm4KOqaAAFqhEXEmcJvB0s836iZsVPVp4DdK30XkBaA3NBBYC3xGRG4nMBDYGQqLe4G/KbMoOwu4SlW3icibInIKgYHACuDvwn3WAhcCXw3/L18bMmqMdcpkmqWNilgnKs2mhoYPXnf8bKrWAtc3X5pmwaXp8/eAR4F3iciAiFwUs/vdwHNAP/C/gU8BhIYBXwaeDP+uKRkLhPvcFB7zawLjAAiEzIdE5Fngg+F3wwHNYn7rkmZqoyLyvBSRf8dy/rjBpTXa+Qnb55d9VuDTEfvdAtxSpbwPOKFK+SBw5gSra2TAtVolj+rJF9Web451ean3OlERsynf/FOaBYsgYGTGZafMo3rySW3VjC+ueq4TFWF1Zzl/3ODMqbPRMKfObLhwGotz5EuTP6YIR7848rRR/9ZdbNi8g8VzZ7Bw1jTHNfUXF+2QNPv1ZXbsO4U7dRqtgQu1Sh7Vk49qq6xtdPUPn2bVYy+NfV+xZB7XLD3RVTXH8O0l62Km6mumTt/avpaYsDFy45N3vK9qq4m2Uf/WXRWCBmDVoy+x4pT5Tmc4PqkgwY1lmK/WZr61fa1xZo1mGFnJY/VUhMWUCzZs3jGh8lrgo+WcC8swH63NfGz7WmMzG8NL8qjnfIoHlZXFEcE0o8prQS1UkLVWA7mYqfo4+/VR/VtrbGZjeEv31C4WzZ2RqbPlOdYHFs6axoollSGUViyZ51SFlvcl7CLcf/fULpaf1FNRtry3J9fv6uPs10cBWGvMGi3ErNEMH6m3NVpWyzlXVoAurQuLWIyPu6ardACu79Os0QyjCVg4a1pdTZ7PXTyH446ZPmEB50oN5FK9VG9rsyQDABfqX5+MDkzYGIYxRtaXkys1ULOol9JawNVSAPpmdWdrNoZhAPksolytg/i4vpIFi/FmMxvDMELyqqxcWQE2g3WhxXizmY1h1IzB3UNs3LyjYX0javFycmUF2OjWhUXM0HybFZo1WohZoxl58GkhNg+uLKKMAN8s4GqBWaMZRp3wbSE2D82gsjIqKSLGWzVM2BhGTga270VHKzUEOqoN6/3ty8up2WiW2W9WbM3GMHJy+KR2hkYqhc3QiHL4pPaCamT4RivEPkvChI3hnEZfOE9iz/4RJndWdqXJnW3s2T9SUI0M3/DNDLkITI1mOKUVVAdR1lq1MDFt5vwmrUQtLP0a/VmwmY3hjFZRHbgyMXUR2NIohrzPSDM8CzazMZzRCmHTS9TaiquZLNyMgKzPSLM8C85mNiJyi4i8JiI/Lyv7uoj8UkSeEpEfiMiMsm1XiUi/iPxKRD5cVn52WNYvIleWlS8QkcfD8u+LyKSwvCv83h9un+/qHo14ivRgLmKdqJaOh6bjb06yPCPN8iy4VKN9Bzh7XNk64ARVfQ/w78BVACJyHHAecHx4zD+ISLuItAN/D3wEOA44P9wX4FrgOlVdCGwHLgrLLwK2h+XXhfsZBVCUB3MzqBx8CzViFEezPAvOhI2qPgRsG1f2L6o6HH59DChlRVoK3K6qQ6r6PNAPvD/861fV51R1P3A7sFREBDgDWBMefyvwsbJz3Rp+XgOcGe5vFMC5i+fwyMozuO2TJ/PIyjOcGwc0yzqRb6FGiqbZLRrjaJZnocg1m/8EfD/8PIdA+JQYCMsANo8rPxnoBnaUCa7y/eeUjlHVYRHZGe7/xvgKiMjFwMUA8+bNG7/ZKCOPJYwLJ8Go+hS5TlRrayHz5g9oBYvGJJrhWShE2IjIfwWGge8Wcf0SqnojcCMEsdGKrIvP+NbZ4+pTlMrBVRu1ujd/syyO14JGfxbqbvosIv8ROAf4Uz0YBXQLMLdst56wLKp8EJghIh3jyivOFW4/ItzfyIBvaqmk+pRUDpPaha6ONia1i3OVg29t5CtZVGHNsjhu1FnYiMjZwBXAuar6VtmmtcB5oSXZAuBY4AngSeDY0PJsEoERwdpQSD0ALAuPvxC4q+xcF4aflwH3q4W2zkyRnb3ayylNffpe2Mb+EWVoeJT9I0rfixVLhzXHXojJZDXaaJbFccOt6fP3gEeBd4nIgIhcBHwTmAasE5ENIvI/AVR1E7AaeAb4MfBpVR0J12Q+A9wL/AJYHe4LsBK4VET6CdZkbg7Lbwa6w/JLgTFzaWPiFKmWqvZySqpP/9ZdrHrspYrtqx59if6tu1JdN8vo216I8fiYAdSoP87WbFT1/CrFN1cpK+3/FeArVcrvBu6uUv4cgbXa+PJ9wB9NqLJGJKXOPj7HSb3UUtX09HH12bB5R9Vzbti8g4WzpsVeN+u6SxFt1Ej4mgHUqC8WQcBIpN6dPenlFFefxXNnVDtlZHmJvAvR9kKMplYZQOvdpo0ei8w3TNgYqahnZ0/zcoqqz8JZ01ixZB6rHj2oSluxZF7FrKbaS6QWJtNZ26jZX2ppZn6+tYFvFpjNgAkbwzvyqqWuWXoiK06Zz4bNO1g8d0aFoIl6iTSbybRvxM38fGsDM7d2gwkbw0vyqqUWzpp2yBpNmrWgz695ivY2YWRUC1+bKgpXs4xqMz8f26CVAsjWExM2hrfUWnWX9BIJ7OMVVIL/HRNlGl3kS63eswwfX+xmXegGy2djtAxxL5HSCHtoWHnrwAhDw+rcMfPwSe3sO1BZn30HRgtLJ12Ec6qPL3Yzt3aDzWyMliFuLWjj5h11H2Hv2T9CV7swNHJwFtXVLoWlky5iluGr2bhZF9YeEzZGSxH1EilihN0zcwrSJlAmbKRNChvVFzXL8PXF3uixyHzD1GhGy1EtgVURqhPf1DVF1qeWiecMPxELGxbQ29urfX19RVfDKJg4SyxXVlpF+JgUcZ+tQiO1Xy3qKiLrVbU3ab9UajQR+X3g/6rqaOLOhlEjiui0UaoTl1ZaedQ1Wdoo6V7MWz87vvkMxVHvuqaa2YjIbcAS4E7gFlX9pbMaFYTNbPzCp047uHuIU6+9v8JybHJnG4+sPKPQF2OWNvLxXnz6rfPgY9tGUcu6pp3ZpFqzUdULgPcCvwa+IyKPisjFIhIf2dAwMuBbfhjf0iyUyrO0kW/pEHz7rfPgW9vGUURdUxsIqOqbwBrgduAY4OPAz0Tks47qZrQovnVa39IsQPY28s2vxbffOg++tW0cRdQ1lbARkaUi8gPgQaATeL+qfgRYBFzmrHZGS+Jbpy3CSitpxJ+1jXyzgOuZOYW9B4YryvYeGPbyBZ2Eb20bRxF1Tetn83HgOlV9qLxQVd8Kk6IZRs3w0dHPtzQLedro3MVzOO6Y6VUDlRaBSGV4oOC730QZNORt23oaStT7mU4UNiLSDrxtvKApoar31bxWRsvjo6Ofb2kWsraRTwvyA9v3MrmjnQMjB2c3kzvavQ56Gdd+edq2iN+lns90ohpNVUeAURE5og71MYwxWtnRL62aY6Jt5NuCvG8q0yTi2i9P2/r2u7ggrRptN/C0iKwD9pQKVfVzTmplGIaT2Z1vUZZ9VJnGEdd+pc9Z2rao36Wearu0wuafwz/DMOpIrdUcPs4kfFSZRpHUflnbNu/v4sK5t9ak9bO5tdpf3DEicouIvCYiPy8rO1JE1onIs+H/M8NyEZEbRKRfRJ4SkfeVHXNhuP+zInJhWflJIvJ0eMwNEq4qRl3DaC2i/FNaHV8tphpFZRrXfnnaNs+xcSbyURShtksbQeBY4L8BxwGTS+Wq+vaYY04jUL+tUtUTwrKvAdtU9asiciUwU1VXishHgc8CHwVOBq5X1ZNF5EigD+glMFdZD5ykqttF5Angc8DjwN3ADap6T9Q1ku7RIgg0Dz4tgPtKs4SHKQpXseUmemzWSAAbN+/ggpseZ9fQQcOMaV0d3PbJk1k0d8aE6lzTCALAt4FvAcPA7wKrgNviDgit17aNK14KlGZEtwIfKytfpQGPATNE5Bjgw8A6Vd2mqtuBdcDZ4bbpqvqYBtJy1bhzVbuG0QIUudDaSLOpRplJ+Epc++Vp24ke20jOvWmFzZTQxFlU9UVV/Svg9zJcb5aqvhJ+fhWYFX6eA2wu228gLIsrH6hSHneNQwhD7vSJSN/rr7+e4XYM3yjKIz2LKsMw8tJIzr1pDQSGRKQNeFZEPgNsAabmubCqqog4zW+QdA1VvRG4EQI1msu6GPWhiBFb+WyqZE10xZ1PcerCo2zmYDglr3OvV06dIZcAhxGskXwZOAO4MPaI6mwVkWNU9ZVQFfZaWL4FmFu2X09YtgU4fVz5g2F5T5X9465htAAuTWmj9Om+mRMbrUUeoVFPp85UwkZVnww/7gY+keN6awmE1FfD/+8qK/+MiNxOYCCwMxQW9wJ/U2ZRdhZwlapuE5E3ReQUAgOBFcDfJVzDcIRvi80uRmxxRgcuZ1O+tW0e6rlw3mo0QgrrWGEjIj+iPGjROFT13Jhjv0cwKzlKRAaALxIIgNVhPLUXgeXh7ncTWKL1A28RCrRQqHwZKAm7a1S1ZHTwKeA7wBTgnvCPmGsYDvDV8quWnS9JTeZqNuVr22ah0cK4GLUn1vRZRH4n7mBV/dea16ggzPR54jRSsqg8pDUTreXou5naNs+9NFM7uKTImV9N0kI3kzAxak+rrFWkVZPVcjbVTG2b516aqR1c0Sgzv7T5bI4VkTUi8oyIPFf6c105w298DH3igiLMRJupbfPcSzO1gwsaKYCnM6dOo/nxNfSJC85dPIdHVp7BbZ88mUdWnjHhkeNEHT6bqW2LCuPSCjRSptO04WrWq+pJIvK0qp5YXua8hnXC1myyY5ZC8eRRczRT25o1Wu3xYU2rJms2ZdTcqdNoHhrB7LIo8jp8NlPb5rmXZmqHWtJIKRrq7dRpGA1LltG1LXAbrmmUFA0TduoUkUuBHZpG/2Y0FFlVFa2g4siqCvN1gbvRfrMi6ttIbdQIM78kp86rgdWq+ksR6QJ+DCwChkXkT1T1J/WopOGerC/TRjG7zEMeVZiPao5G+82KqG+jtVEjkGSN9sfAr8LPJbXZ0cDvAH/jqlKGO6pZRWU1n0x7XNbQ+3HH1TOcf16Ln7yWbLWkkUxlIV19a/0sNFobNQpJarT9ZeqyDwO3q+oI8AsRSbveY2TAxRQ+arSWdV1hYPtedLRSm6qjWnGcixlTvUedtVCF+aLmKHINycWa110btnDFmqdobxNGRpWvL6t8FmydzR91YJLAGBKRE4CtBP41l5dtO8xZrVocFy/TOFVQ1pfp4ZPaGRqpFDZDI8rhk9oTrxn30McdB9Q9nH/31C6W9/aw6tGXxsqW9/Z4/+Kp9pIpag3JxZrX4O4hLr9jIwfKnsHL7tg49iw02zpbFnxSByap0f4CWAP8ErhOVZ8HCNM4/5vjurUkrqbwcaqg0su0nDQv05d3Vlcjlcqj1ExJ6qe444pwYhvcPcTqvoGKstV9A16rVaKSuRXhJJnnmY6r76aXd1YIGoADI8qml3c6u2Yj4Zs6MCk22mPAu6uU300QqbnlqbWjmqspfNIIsdrL9JIz3zl2zer3KRFXC8oPn9Re4WwGsO/A6NjMJ4q442YePinVqLOWqoNGU6skzSjrbSqbt/2i6xv9/Lm7ZuPg23ObZI12adx2Vf1GbavTWCRNUeNeeFHHuprCx1lFbdy8I1EvXq2ux8+eTkcbDJdVt6MNjp89HYA9+0foapcKVVtXu7Bn/0hsXeOOWzgr2bqr1qqDRlOrpHnJ1HMNydWa1/Gzp9MmUL5s2CYHn79mWWfLim/PbdKazbTw/3cBv0mQmAzg94EnXFWqEUgaPca98JKOdWUqGzVaS5r1xNX1G8sX8/k1G2mXNkZ0lK8vW1Rx3pFx7lgjqokPe8/MKUibQJmwkTYZOy5u1OkiRbOP5stx+PaScdl+1YSN62s2Cr61QZIa7UsAIvIQ8D5V3RV+/yvg/zqvncfEjR4hfhE7aeRZ7yl8nlnPuYvncNwx09mweQeL585g4axpFecWEcrz7wXfs9enfJ9q7eJKddBIahXfXjLgpv0Gtu9lSmdHRZ6hKZ0dhfUjH/GpDdKaL88C9pd93x+WtSxxo8ekF16akaeLKXzcbCtu1rP3wHDFefYeGB6ra9w5B7bvpb1NKhZx29uk4sXfv3VXVUGVtZO4HNU3klrFp5dMiVq3X1H9qJmop1l0WmGzCnhCRH4Qfv8YcKubKjUGSaPHuE5QxMgzjXopqmNGzU6SzplkIHD1D59m1WMHzYlXLJnHNUtPHPue5UXh46i+KJr9RWu/dTI++auljY32FRG5B/hAWPQJVW150+coFVKaTnDu4jnMPmIyDz37BqcdexS9C7prUqeokUoex83JHe0cGDk4u5nc0T6mLow7Z9xCf//WXRWCBmDVoy+x4pT5h6jiJoqPo3rDzSi6qN/aF0fJOHzzV5tIFIDDgDdV9dsicrSILCj53bQqWdRSJcpH9Tfc33/IqD6OqAc9rj5Z1UtJx8Vti1vof+CXr1W93obNO3ILG2j+UX2j4XIUXe/f2idHyTiS1pXrbRadNi30F4GVwFWlepEjU6eI/KWIbBKRn4vI90RksogsEJHHRaRfRL4vIpPCfbvC7/3h9vll57kqLP+ViHy4rPzssKxfRK7MWs840jhMdU/tYtHcGYf8eFGj+v6tuxKvG+Wsl1SfrI5qcQ6fSeeM27547oyq14sqNxoX35wL89BI9xI3UCzCYjHtzObjwHuBnwGo6ssikmn4KSJzCPLiHKeqe0VkNXAe8FGCKAW3i8j/BC4iSEV9EbBdVReKyHnAtcAfi8hx4XHHA7OBn4jIO8PL/D3wIWAAeFJE1qrqM1nqG0Ueq6cNm3dElseN6uOmxWnqkzTbqjZjSnL4TDpn1PaFs6axYsm8ihAwK5bMq7j/RlBVpCXKEALc3WfceePqU2t8cy7MQyPdS5I6v97rXWmFzX5VVRFRABE5vAbXnSIiBwjUc68QJGT7k3D7rcBfEQibpeFnCELnfFOCFeqlBIFBh4DnRaQfeH+4X7+qPhfW9fZw35oKmzwjg6yj+rgHPW19olQOUQENB7bvZXik8rzDI6M1cRA86W1HcvsTLyG0oYzS+7Yjx9Wn0n+naFVFVqEQZwiRxzE4jrj2SzLMyINP8dhc0Gj3EjcYrPd6Vyo1GrBaRP4XMENE/hz4CXBTlguq6hbgb4GXCITMTmA9QUK20ir0AFDqcXOAzeGxw+H+3eXl446JKq8pWdVScHBUX874UX014h70PPUpBTQcGh7lrf0jDA2PctkdGxncPcSB4ZGKCAEQRAw4MBwfBaBEktpv/wgMjYyyf4QxdcTg7iEuW72BoWHlrQMjDA0rl67eUKiqIuo+kohTmSapZLJeM6798qhwk4iLx5Yl9p6P5OlnRRGlzk/aVmvSWqP9rYh8CHiTIJrA1aq6LssFRWQmwUxjAbADuAM4O8u58iIiFwMXA8ybNy9h70PJMzK4ZumJrDhl/oRUGUnT4qz1iQto+Nqb1V/wLwy+lWhBl1Xtt3PvgaoCbtPLb3LaO49OdU+1JE9Ugof734gsf++8mZkdg8vrNv733vTym5Ht99zruyPrk0edlmT5lBR7r5Ewa8dspBI2InKtqq4E1lUpmygfBJ5X1dfD8/wzcCrBrKkjnL30AKVh3BZgLjAQ5tA5AhgsKy9RfkxUeQWqeiNwI0Bvb2+mNNd5LGEWzpo24Q6e9KBnq090QMM8C/lZ1X479+4ff6qQYjKR59HTHzV1UmR5HsdgiFPBRbWTclREfaPK0+Kb5ZNrzNpx4qRVo32oStlHMl7zJeAUETksXHs5k2A95QFgWbjPhcBd4ee1HMwSugy4P0zothY4L7RWWwAcSxCv7Ung2NC6bRKBEUEppltTUOupbymgZjmlgJpZVX6QXe13/Owj6GyvFICd7cLxs4/IdoM56Zk5hX3j1Ib7hkdS6enf/R+mR5bHtUFS5IY4FVxc+y15RzftbZXb2tuEJe/I5+flm+WT4R9JUZ//C/Ap4O0i8lTZpmnAI1kuqKqPi8gaAsu2YYK8ODcSxFq7XUT+Oiy7OTzkZuAfQwOAbQTCA1XdFFqyPROe59NhFlFE5DPAvUA7cIuqbspS17w0ijVV99T4gJpZVH6l82ZR+3VP7eK//9EiPj/OYCFJfeQSHRdQdPz3KF7euS+yfOGsabEz1bi4cnEziUVzZ8S233XLg20lxrdtFnyzfDIO4st7KEmN9k/APcB/A8r9VXap6rasF1XVLwJfHFf8HAetycr33Qf8UcR5vgJ8pUp54fl2GsXxq0SSei6Lyi/NebMcV++2TQr4WKJ6p45WaZWoppKJi9xQmvnEzRaSrJDigqdmxSfLJyPAp/dQUtTnnQTWX+cDiMhvAJOBqSIyVVVfiju+VXER5r4euNJDx5lbx3WEascV0bY9M6ewZ3+lSmvP/uEKNVB0zp8jInKuxKsEk1R33VO76H3bTB7uHxzb/ptvm1nRBlnbPQ9xz5Ctc9QX395DaSMI/L6IPAs8D/wr8ALBjMeoQtrUxYO7h9i4eYeX3seuyeqJXURa6O179lcICwiEx/Y9gSFD0r1UWyNJQ5zqrn/rrgpBA/DT/sFEE+YiPeDzPO9xx7ZKP5rofRbRV+JI69T518ApwE9U9b0i8rvABe6q1dikWRD1aXpbBFktvPIs1mclKeJDkiVWUpqFaiSp7rJGoSjKAz7P8+5T5OKiyHKfvhlmpLVGO6Cqg0CbiLSp6gNAr8N6NTRJjl9pRpe+jdZqXZ88HSHrYn0aqt1nkvl33L0kpVmIIskaLY1J+n3PvMrKNRu575lXK85bb2GdZzYVd2yjztKyXCvLffrmgJp2ZrNDRKYCDwHfFZHXgD3uqtX4xC2IJo0ufRutuahPkvVSFGkX67MQdZ8zD6/uK1Mqj7uXge176Wijwsmyow327E+OwBBnjbZw1jQ+sLCbn5ap0j6wsHtsVnPWdQ/y71uDLvr9vgHeNetw7v3L0wG3wroaeWZTPvrvFGGgkvU+fTLMSCtslgL7gL8E/pTAsfIaV5VqFqIWRONGwr4t6rmsT5aO4Eo1EHefj/56sOoxj/56kHMWzY69l8MntVcpCiA3AAAgAElEQVT15i+f2VQLiplkjTa4e4gnX9xecd4nX9zO4O4hNry0fUzQlPjV1j3c98yrHDVtsjNhHUWe3yxPigsXFGWgkuc+fTHMSKVGU9U9oQ/LYcCPCNILFOPO3UBETbXjpre+LeqlqU8elcJEHVS7p3ax/KTax9mKu883dlf3lRlfXu1e9uwfqeowW5rZXP3Dp/ngdQ9x+Zqn+OB1D3H1XU8DyRZwA9v3ouOsFnRUGdi+l395ZmvV+v7LM1sL0eOnUedk6StFqIlc94dq+KYOy0racDX/GfgSwexmlCC+iQJvd1e1xiZpqh01EvZtUS+pPvVWKQzuHmL1+trH2Yq7zwPD1c2UT0gR0SBuZhOXrRSItIDrnhqk3B4aF89uaEQ5fFI7S95+JN8fF4sMYMnbjxwT1uXXrUdQzDx+Uz757xTVH3xSh2UlrYHA5cAJqjpfVd+uqgtU1QRNBGkX9KqNhH0bxcTVp4gF2lrM/KqNPOPus7OjnXHRX2gX6OyIX+SH+AgCcRZlcdsgmBlN7qxsh8mdbezZP8KCo6tboy04elqksK7HQne15z1PX0mzzcU9FNUf6nmfLki7ZvNr4C2XFWlUqnmN5zUvdeXhnZWoUVURZrR5Z35ZUnn3zJxCZ0cbI2VWZZ0dbSmvGR1BIEuQ03ILuGqUyid3tlVYwU3ubEsd4LOe+FafNPjUHxqJtDObq4D/JyL/S0RuKP25rFgjEJW/oxYvxHO++TBf+tEznPPNh1PnMXFJtVFVUfr/rLlRsqbyzjPbjAuKGRfkNCkAata1jEZT0/qKL/2hkZA0Zo8i8gTwMPA0HBTbqnqru6rVl97eXu3r60u9/+DuIU699v5DRo+PrDyD7qldrN2w5RBT2DS626Tz+kbW+8xKnvbZuHkHF9z0eIUl1rSuDm775MksSpEyIWtAw7UbthwSFLO8jeJSNCelb46rU9S2ev9mSfhWnzw0072kRUTWq2qi32VaNVqnql6as05NRdKUOeuCXt6peL0jvNZ74TJP+xRlQponyGlSANQssch8W2z2rT55aKZ7qTVphc09YVbLHwFjOoc8kZ8bnTQvriwvpzwvxKKcQetpx5/kWR9HVkfSWuCLr0MJq487muleaklaYXN++P9VZWUtbfrs6sWV9by+OYO6JM6zPok8I09Xs8Y85816bJJ6rpHwJV+LEU8qYaOqC1xXpBFxNWXOct5WsYRJ8qxPQ5aRp6tZo6sAlXFc/cOnK/xsViyZxzVLT8x8D0XiW2gnI5pYazQROSP8/w+q/dWnin7jyvZ9oudtFUuYIu7Tlf+EqwCVcUQ5kialJvCRIgNxGhMnyfT5d8L/f7/K3zkO62XEEOeU2NUhHNbZTleHNGRIiyR8DVEC9c03kjVsysP9b1Q9X1S5z/gW2smIJylTZyl18zWq+nz5NhEx1VoBxKkNglUMCYMJpV/H8JUoXbxvIUogWZ1T7V5cBqiMqs9REW0VVe4zrTKbbxbSOnXeWaVsTS0rYiSTJrfH0PAob+0fYWi4sVUKUQ6zJXwJUQLJ6pyoe8kzS8saNmXJO7qrZg5d8o7uGreae3wL7WTEEzuzEZF3A8cDR4xbo5kOTM56URGZAdwEnEAwIP9PwK+A7wPzCdJOL1fV7RKYGl0PfJQgZM5/VNWfhee5EPj/wtP+dcnJVEROAr4DTAHuBi5R10k76oCPuT3yUm3E76NlXVwIoaTfJe5ezl08h9lHTOahZ9/gtGOPondB5Us/ztIqqk5x9Vk0dwbXLV/E59c8Nbbt68sa9wVtfi2NQ5I12rsI1mZmEKzTlNgF/HmO614P/FhVl4nIJILUBV8A7lPVr4rIlcCVwErgI8Cx4d/JwLeAk0XkSOCLBBlDFVgvImtVdXu4z58DjxMIm7OBe3LU1wt8y+2RlyhVj2vLuiymsndt2MIVEVEA4n6XpHsptwy74f7+CsuwJNVcUKeNtEsbIzrK15ct4tzFcxKfk2Z7QTeTX0uWiBCNQqwaTVXvUtVPAOeo6ifK/j6nqv8vywVF5AjgNODm8Br7VXUHQYK2UvibW4GPhZ+XAqs04DFghogcA3wYWKeq20IBsw44O9w2XVUfC2czq8rO1dBkjYdVNP1bd7Gmb3OFxVOcqselLj5JPVeNwd1DXH7HxgoV5WV3bBxTk3VPjc6xE3cvcZZhSaq5wd1DXLZ6A0PDylsHRhgaVi5dvYHB3UOp4scVEUHYt1TnvhH3bGZ5bn0jrVPnx0VkE7AX+DHwHuAvVfW2DNdcALwOfFtEFgHrgUuAWar6SrjPq8Cs8PMcYHPZ8QNhWVz5QJXypsCn3B5piPLpSFL1uHCYzaqe2/TyTg6Myx1zYETZ9PJOTnvnbyTm2Im6lwd++VrV623YvINjZ02LTI7WPbWLTS+/WTVPzqaX3+T42dP53hObK7Z974nNuXP+5MH8YeKJezYhXhXbKKQVNmep6hUi8nGC9ZQ/AB4iyNiZ5ZrvAz6rqo+LyPUEKrMxVFVFxPkaSxiC52KAefPmJeztD1niYZVwMRWP8kaPSw6WV9WT5T6yqufe3HsgtjxrnLz53YdVPe/87sNik6Ml1SlJONYbH9fgfKMZ12PHkzoQZ/j/7wF3qOrOiYQIGccAMKCqj4ff1xAIm60icoyqvhKqwkrDvi3A3LLje8KyLcDp48ofDMt7qux/CKp6I3AjBFGfs95Qo+BidBnnjR6XAGxZ79zE2UuU4Mx6H1nVc9OnTIotz3rezo52OtqomKF0tAXlpeRo46Nbl9JJT5/SOf50seUBxZjDt0p0izw023psNdKaPv9IRH4JnATcJyJHE6SInjCq+iqwWUTeFRadCTwDrAUuDMsuBO4KP68FVkjAKcDOUN12L3CWiMwUkZnAWcC94bY3ReSU0JJtRdm5WhYX3tZJ3uhJycHOXTyHR1aewW2fPJlHVp6ROgVD1vvIuq41+4jqhpel8qTzxuU96miv7IId7UGSs6TkaMfPnl51+/Gzp3P87Ol0jOvZHW3Rx7jG/GGSadT12ImQNjbalSLyNYIX/YiIvEWwcJ+VzwLfDS3RngM+QSD4VovIRcCLwPJw37sJzJ77CUyfPxHWaZuIfBl4MtzvmrIo1J/ioOnzPTSBJVpeXIwuH+5/PbK8PAHYqkcrZz7lqraJWhLVIgvqRNe14lI7l+4l6rxJKqS42V3ctudf3121Ts+/vpveBd18Y/liPj/OUq2ol1OR0bYbiUZbj50oSX42V6jq18KvZ6rqHQCqukdE/iuBufKEUdUNBCbL4zmzyr4KfDriPLcAt1Qp7yPw4WlKsqxXuBhdHjW1+oi/vPyapSdy7ntmR/qRTJRa3MfETWWjUzsnnTfNek6U/07cC+ahZ6uHl3no2TfoXdDt3cvJt/r4Sp71WN9JUqOdV/b5qnHbzq5xXYwUZDWB7J7aRe/bZlaU/ebbZuZ6eJe8o/uQVQAJy8vre8EtT/DtR17gglueyG2yWYRK4fjZRzDO6Z42CcqT6Jk5hX3DIxVl+4ZHKsLKxKUAjzJRPu3Yo6per7y8CPPmOHyrj1FfkoSNRHyu9t1wTJ71iv6tu3i4f7Ci7Kf9g7mi/XZP7eL68xbT2QadbUJnG1x/3uLUYVyykmWtJy/VQryMJ8qPZHzwitL3PO3Tu6CbDyysnCV+YGF36pljNd8nw3BJ0pqNRnyu9t1wTJ71ijjLsDzJsxRoa2sb86yvVX2TqKdKIU0OnbhoCFM6O9g1dPDYKZ0dNTFp/cdPnkLf84MTVlE2Uz4bo3FIEjaLRORNglnMlPAz4ffMsdGMbORZr0iyDMtCefDPEuWL381ihZSkCoszAkhKY523fXoXpJ/NQLzvU6Nn7DT8JilcTbuqTlfVaaraEX4ufY8z6G8Z6hmCI896RckyrJzxlmFxVLvPpHwizWKyCdGqMEhuh/E+aaXvrtunmqqsmfLZGI1FWqdOowpFhODIY9VzzdITWXHK/Annno+6zzQzFx+tkCZqzRenCivN4KJmPgPb9x4yomsLz5lkjZaHKFWZr/lsGj3IpJGMCZuMFBmCI896Rcn/JS15/ERqUd9ak2WAkEaoRs18ksLOuBiwxKnKSvlsytfXis5nY3HTWoO0EQSMcbRKStqk+yzCMiwrWa2/SkJ1UrvQ1dHGpPbKlNulmU85pZlPKexMOaWwM66s9eKcbbundnHd8kV0dbSN/V23vDiHT1dtYPiHzWwyUovF70ZQHaS5T1czl1q3Tx7ruL4XtrF/RCkZYfa9uK0in02cEUA1Siq28RZ8I2WRnbOS5Gzrk2pzYPve2OjWRvNgM5uM5F3cbZT8FEUt8rton6wDhKQYcJDNCODA8EjV6MwHxq3/TJQ0zra+OFgmqRmN5sFmNjnIOkJ0ud7jYrZU75Gwq/bJGqMryUcpyQ8nqv1eGHyr6nlfGHwrV1ifkrPt5XdsQGhDGeVv/2hx4YKlGi/vrK52fnnnXjPFbjJM2OQkiwrJlbOjy4XWeqrKXDqDZhGcST5KWVWNtfB9ihpc+KQqiycqEIkFKJkIjaCSN2FTAC6cHRsxQVUek+o8TFRwLpw1jQ8s7OanZeF+PrCwe2zknXXGlCYqdhxJgwufrACjOH72dITKcCRCcekQGpFGseYzYVMALkKuN1qCqlqYVNezrk++uL2i7MkXtzO4e2isTllnEll9nxpxcBFFR7tUrF11tNusJi15n4N6zohM2BRErdUcjRYaJmsqZR/rWiLrTGKivk9p61SEaiWLw2xS3DkjmjyDzHrPiEzY5CRPh66lmsO32UA51dqoSJPqieKjIE+qUxGqFVcOs3lohLWMPGRtvyJmxiZscuCbrtSn2UCJqDbyWTiOp3tqF8t7eyrWVpb39hRa17j2K+JFkvWaLp8D3/qnC7K2XxFqdxM2GfFVZ+6Tg2VSG527eA6zj5hcsyyeaYm7l/6tuw5ZPxncPcTqvoGK/Vb3DXDJme8s9LeOGlwU8SLJc00X8eF87Z8uyDLILGK2bsImI422IJ+HrCPEpDYqDxZ5w/39dcmrEncvUcEri/ytqwm/cqoNLop4keS5posZSCv1T4gfZFYbXJVmRJffsRERQVWdaxYsgkBGfNTjuyBP7Kq4NkrjlV9r4u4lrj5F/dZX//BpPnjdQ1y+5ik+eN1DXH3X06mOKyLqQ9ZruoqN1ir9M4m4SBylEExDw6PsH1H6XtzmtC4mbDJSVBiXepMn4GhcG8V55bsi7l7i6lPEb51XGBcRIDXpmllyIsUdG0er9M84sg6uXFGYGk1E2oE+YIuqniMiC4DbgW5gPfBnqrpfRLqAVcBJwCDwx6r6QniOq4CLgBHgc6p6b1h+NnA90A7cpKpfdXEPPi7I15q8I8SoNnKROTSJuICZUbG4SvWp929dizTeRVjzRV0zjwNvVjVbK/TPOOJUic9GCJW8aeLjKHJmcwnwi7Lv1wLXqepCYDuBECH8f3tYfl24HyJyHHAecDxwNvAPItIeCrG/Bz4CHAecH+7rBF8CGrqiFiPEam2UN3NoVqICZqapTz1/6yKEsSviRthJz1deNVuz98844gR5Ec9XITMbEekBfg/4CnCpBD3+DOBPwl1uBf4K+BawNPwMsAb4Zrj/UuB2VR0CnheRfuD94X79qvpceK3bw32fcXxbTYurEWJW7/msJDkQJtWnnj4beUPZuCSL42ZWB15fnVezUs+6xplFd0/tqvvzVZQa7X8AVwClO+sGdqhq6S0wAJTmyXOAzQCqOiwiO8P95wCPlZ2z/JjN48pPrlYJEbkYuBhg3rx51XYxQlypZLJ4z2cljcomqj53bdjCFWueGsty+fVl7n026i2M0+DKcTPq+SrSebXWgqGIusYJ8no/X3VXo4nIOcBrqrq+3tcej6reqKq9qtp79NFHF10dwzF5LKYuv2MjQ8OjvLV/hKHhUS67Y2NdskkunDWNZb1zvRA0eTOdZlHFxh3rMstnrfMpFVnXOFViPZ+vImY2pwLnishHgcnAdILF/Bki0hHObnqAUottAeYCAyLSARxBYChQKi9RfkxUuVEAPqk5sqgEN728s2qSs00v7+S0d/6Gq6p6R17Hzayq2Ho7r7pwCG2kurqi7sJGVa8CrgIQkdOBy1X1T0XkDmAZgUXahcBd4SFrw++PhtvvV1UVkbXAP4nIN4DZwLHAEwQRyo8Nrdu2EBgRlNaCvMKnl7ArfAwZMnGVoOVcgfyWiXlUsVmdV7P0MReCwZXfTyM5r/rkZ7OSwFign2BN5uaw/GagOyy/FLgSQFU3AasJFv5/DHxaVUfCmdFngHsJrN1Wh/t6RaOkhc6DS9VBPTl+9nQ6xvWUjrbWy7nim+9K99Qulp/UU1FWHrMuax9zIRhctV0jOa+Kqibv1QL09vZqX19fXa41uHuIU6+9n30HDj4kkzvbeGTlGd6NRkpkGSFu3LyDC256nF1DB62/pnV1cNsnT2ZRg5nwrt2whc+v2Ui7tDGio3x92aLCZ2hF4Uvqgrh+BOTqY2s3bDnEiqsWv7eLtnNV17SIyHpV7U3az2KjFUAjTX0huyrM5air3i+8VncQLMeFZWLc7xn1/MX1o9LnrH0s6ffO+vy5aLs8z6YlT2tyGmnqm2cBMs7OPw9FrQMV4ZHfCsT9nnHPX1I/ytvHJhoNoUiyPJv1vg+f1mxaBt903yXyxK6KotYxunxeB4qL3zXR2F6tQtLvGff8xfUjV32syOevls9QEfdhM5uCKEotEzVtzhO7qp74qoKMGyX6OBJ2RZxaptq2pN+zZ+YU9uyvjGe3Z//w2PMX149c9LGinr9aP0OWPK3FqLdaJuqBTVKVLT+ppyJC7PgslVn07VmphfCrtZ46rv2AhvGDyEsWgZv0e27fs5/RcTZMoxqUl9ovrh/Vuo8VMfhy4UtTxH2YGq1FiJs2x6kqBncPsXr9oVkqS9PtOPNSF1P1vOoRFybnce2XVw3ZKMT91nkCcRaRiiKOIlTgLp6hIu7DZjYtQty0OW6Uk2TxEzficjVVz6oeceVt7XqhOiv1tDTKYxkWlxbax+jX9VaBu5qF1Ps+bGbTIsQ9sHGjnLgcMEkjLpdT9bh4T1G4mmUUsVCdRL2dhuN+6zTBNM/55sN86UfPcM43H66o68JZ0/jAwu6KYz+wsLvwWHFZnr8818rzDMUZFtTzPmxm0yIkmSHHjXKCjA467nuyMHFl+pwVl8Kv3gvVcRQRLyvpt47allTXwd1DPPZ8Zbrix57fNqaCaxWyPkM+GaeYsGky4lQnSQ9stcXUuBwwi+bOSBQmrpzjslB6IX6+LFVALYVfPReq4yjKYipJ4FZTlSXVNU0Q1P6tu7xKw+CKiT5DvgXpNGHTgEzUfDkPSbOBNCMun5zjtPSvVs7W0tAogVOLNFef6G+dXNf4IKhX//DpCkvJFUvmcc3SE2txKw2Pb24CtmbTYETp4tNYfmXR46fRF2fR+xbhVFa65tCw8taBEYaGNfU1Gylwqm9Ow3ms0eKCoPZv3VUhaABWPfoS/Vt31evWvMY3Hzmb2Tiknv4cSaOYPFPqZnGOy3pN39QRafDJaThPWujuqV18Y/niQ4Kgdk/t4oFfvla1Dhs27yhUneZqBjzR8/q2ZmrCxhEu0ghnNV9OOjbtg9voznFZ85/4po5Iiy9Ow3nSQkO04PTRLNqVajjreX0KIGtqNAe4SiOc1Xw56dgiKELVk3TNKFVZnPm3EZBHVZaGaqrahbOmsWLJvIr9ViyZV9isxpVqOO9562neHIfNbBzgKo1wHvNl36bUSfWt9zWTQs5EmX8bAXlUZXm4ZumJrDhlvhfWaK5mwI06sx6PCRsnpEsjnEW3m8V8ufzYKE/toqi3qifqmkke8FHm343U2V2Sd+acZ51j4axpmZ7lWq+tuNIeuEp/XW9M2DigZEEzXPZ8jE8jnEe3m/UF7ZODl28kdeh9wyMV2/YNj5garYykmbNvUbFdXNOV9iBP2/qEpYUOqXVa6Lg0wkWkhU5zzUYYHbkkKr3u4O4hTv6bnxwyeHj8Cx9syXaKo+/5QR569g1OO/YoehcEYWZcpm/Oguv+V09rNB9SzFta6IKJU1n5aPbbKKMjl0SpKAe276VdhOGyNZt2EVOjjaPcwfKG+/vHHCwHtu9Fx+UJ0FGtSfrmLKTtfz6lfo46byOt59TdGk1E5orIAyLyjIhsEpFLwvIjRWSdiDwb/j8zLBcRuUFE+kXkKRF5X9m5Lgz3f1ZELiwrP0lEng6PuUEKWM2NCy7om9mvz9kv6001y53DJ7UzNM7gY2hEOXxSe72r5y1xDpZx7edbXyjRKE68vlmZxlGE6fMwcJmqHgecAnxaRI4DrgTuU9VjgfvC7wAfAY4N/y4GvgWBcAK+CJwMvB/4YklAhfv8edlxZ9fhvsZIenm7NPuNivAad8280ZCbPeXxnv0jTO6sbJ/JnW3s2T8ScUTrEZd3Jq79Ss9lV0cbh01qp6ujtibw1Z7NpP7XSIMv36JFxFF3NZqqvgK8En7eJSK/AOYAS4HTw91uBR4EVoblqzRYXHpMRGaIyDHhvutUdRuAiKwDzhaRB4HpqvpYWL4K+BhwTz3uD9JNbV2YgiapwqJUe3lGR62gfuuZOYWRcWqgkVH1cvRYFHEOljMPn1R1W6n98sSriyPu2Yzrf42kmgK/HDfjKNSpU0TmA+8FHgdmhYII4FVgVvh5DrC57LCBsCyufKBKed3omTkllfVSLZ2t0sZGq6bayzo6aqQRYF7GG9KYYU0lcQ6Wcc9Xnnh1caR5NqP6XyOppkr44rgZR2EGAiIyFbgT+AtVfbN8WUVVVUSc92YRuZhANce8efMS9p4YLl9OWUKqJMX3yjI6KnIEmLR4W8uw8wPb9zKls4NdQwf9bKZ0dng70i2KOAfLOOML3xwhfXSAbgYKETYi0kkgaL6rqv8cFm8VkWNU9ZVQTVaKsrcFmFt2eE9YtoWDardS+YNheU+V/Q9BVW8EboTA9DnHLVXg8uWUNf5Ums4XZ0VT7eXuegSYNZVCrcPON+JItyjiHCyrPV9FOkLG0SiqqUaiCGs0AW4GfqGq3yjbtBYoWZRdCNxVVr4itEo7BdgZqtvuBc4SkZmhYcBZwL3htjdF5JTwWivKzlUXatGBqi1s5ok/lXdd5re+eh/n3/gYv/XV+3Kr39KQNZWCi7DzjbQI22i4altX8diM7BQxszkV+DPgaRHZEJZ9AfgqsFpELgJeBJaH2+4GPgr0A28BnwBQ1W0i8mXgyXC/a0rGAsCngO8AUwgMA+pmHAD5p+FRI/e8odqz1Glw9xCXrd4QOjQG61CXrt6QS/2WRJ5UCnFWUXnUaTbSdYertrXfzC+KsEZ7mOjgYWdW2V+BT0ec6xbglirlfcAJOaqZm6wPetyL1lWo9jg2vfxmhec8BGF4Nr38Jqe98+jEa2YhTyoFl2Hni4jj1irU0xHSKAZLMeCQLNPwOJ+XYlQDUUtZ7uw34qz5uqd2sfyknopty3t7xu7Ht7DzhmEEWLgaz0gauddbNXBYZ3Uv+ajyWhFlzTe4e4jV6wcqtq3uG+CSM9851hY+hZ03DCPAZjaekWb2Us+FyxcG35pQeS0oWfOVU7LmSxvtYOGsaSzrnWuCxjA8wWY2HuLTwmYRqXeTZndmhmwYjYfNbDzFF7PLItZA4mZ3ZoZsGI2J5bMJqXU+m2ajlh75aYmLEtDquXcMwxcsn41RU7Km3s1DnNmqmbQaRmNhajTDMAzDOSZsDMMwDOeYsDEMwzCcY8LGMAzDcI4JG8MwDMM5ZvocIiKvE0SbrjdHAW8UcN1GwdonGWujeKx94snbPm9T1aOTdjJhUzAi0pfGRr1VsfZJxtooHmufeOrVPqZGMwzDMJxjwsYwDMNwjgmb4rmx6Ap4jrVPMtZG8Vj7xFOX9rE1G8MwDMM5NrMxDMMwnGPCpk6IyFwReUBEnhGRTSJySVh+pIisE5Fnw/9nFl3XohCRySLyhIhsDNvoS2H5AhF5XET6ReT7IjKp6LoWiYi0i8i/icj/Cb9b+5QhIi+IyNMiskFE+sIy62chIjJDRNaIyC9F5BcisqQe7WPCpn4MA5ep6nHAKcCnReQ44ErgPlU9Frgv/N6qDAFnqOoiYDFwtoicAlwLXKeqC4HtwEUF1tEHLgF+Ufbd2udQfldVF5eZ9Fo/O8j1wI9V9d3AIoJnyXn7mLCpE6r6iqr+LPy8i+AHngMsBW4Nd7sV+FgxNSweDdgdfu0M/xQ4A1gTlrd0G4lID/B7wE3hd8HaJw3WzwAROQI4DbgZQFX3q+oO6tA+JmwKQETmA+8FHgdmqeor4aZXgVkFVcsLQhXRBuA1YB3wa2CHqg6HuwwQCOlW5X8AVwCl3NjdWPuMR4F/EZH1InJxWGb9LGAB8Drw7VAVe5OIHE4d2seETZ0RkanAncBfqOqb5ds0MA1safNAVR1R1cVAD/B+4N0FV8kbROQc4DVVXV90XTznt1X1fcBHCNTVp5VvbPF+1gG8D/iWqr4X2MM4lZmr9jFhU0dEpJNA0HxXVf85LN4qIseE248hGNG3POHU/gFgCTBDREpZZXuALYVVrFhOBc4VkReA2wnUZ9dj7VOBqm4J/38N+AHBoMX6WcAAMKCqj4ff1xAIH+ftY8KmToS69ZuBX6jqN8o2rQUuDD9fCNxV77r5gogcLSIzws9TgA8RrG09ACwLd2vZNlLVq1S1R1XnA+cB96vqn2LtM4aIHC4i00qfgbOAn2P9DABVfRXYLCLvCovOBJ6hDu1jTp11QkR+G/gp8DQH9e1fIFi3WQ3MI4g6vVxVtxVSyYIRkfcQLE62EwyEVqvqNSLydoKR/JHAvwEXqOpQcTUtHhE5HbhcVc+x9jlI2BY/CL92AP+kql8RkW6snwEgIosJDEwmAc8BnyDsbzhsHxM2hmEYhnNMjWYYhmE4x4SNYYmVVxoAAAGdSURBVBiG4RwTNoZhGIZzTNgYhmEYzjFhYxiGYTjHhI1heICIfExEVEQsYoLRlJiwMQw/OB94OPzfMJoOEzaGUTBhvLzfJkgNcF5Y1iYi/xDmHFknIneLyLJw20ki8q9hoMl7S2FGDMNnTNgYRvEsJcgv8u/AoIicBPwBMB84Dvgzghhxpfh6fwcsU9WTgFuArxRRacOYCB3JuxiG4ZjzCQJqQhB25nyCvnmHqo4Cr4rIA+H2dwEnAOuCcHu0A69gGJ5jwsYwCkREjiSI3nyiiCiB8FAOxvc65BBgk6ouqVMVDaMmmBrNMIplGfCPqvo2VZ2vqnOB54FtwB+GazezgNPD/X8FHC0iY2o1ETm+iIobxkQwYWMYxXI+h85i7gT+A0HukWeA24CfATtVdT+BgLpWRDYCG4Dfql91DSMbFvXZMDxFRKaq6u4wPP4TwKlhPhLDaDhszcYw/OX/hMnkJgFfNkFjNDI2szEMwzCcY2s2hmEYhnNM2BiGYRjOMWFjGIZhOMeEjWEYhuEcEzaGYRiGc0zYGIZhGM75/wEyLRJ1QU5ACAAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "# Scatter Plot\n",
    "df.plot.scatter(x='Age', y='EstimatedSalary')"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 27,
   "metadata": {
    "slideshow": {
     "slide_type": "skip"
    }
   },
   "outputs": [
    {
     "data": {
      "text/plain": [
       "<seaborn.axisgrid.PairGrid at 0x7fe3c2c21588>"
      ]
     },
     "execution_count": 27,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAiMAAAIUCAYAAADIVSykAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzsvXuYFOWZ//19qqoPNd0DPQwzgzIDKhnBiTsKQ5RDroTIrjErxjWDhwh4iMtBYszmgLC7siaLvi9IfE3YBAb9GQ+gEQKyurpBXRI2v9UcZCBhzSgiKBkIMMMwg3Po6e6qet4/uqvoQ1V39XT39GHuz3XNBV1d9dRT3TXTd9/f53vfjHMOgiAIgiCIfCHkewIEQRAEQYxsKBghCIIgCCKvUDBCEARBEEReoWCEIAiCIIi8QsEIQRAEQRB5hYIRgiAIgiDyCgUjBEEQBEHkFQpGCIIgCILIKxSMEARBEASRVygYiXDddddxAPRDP2Y/eYfuT/pJ8pN36P6knyQ/tqBgJMKZM2fyPQWCsITuT6KQofuTyBQKRgiCIAiCyCsUjBAEQRAEkVcoGCEIgiAIIq9QMEIQBEEQRF4p+mCEMeZjjO1gjL3PGHuPMTaTMTaGMfYmY+xw5N+KfM+TIAiCIAhzpHxPIAv8CMBuzvl8xpgTQBmAfwKwh3O+ljG2CsAqACvzOcl8c9Gq19La/+O11+doJkShoWkcXf1BBBUVTklEpccJQWAAAEXR0NEXQEjV4BAFVHmc6BlUTPfN91yHejyAjMYkiJHE4KCCLn8QisYhCQyVshNud+ahRFEHI4yx0QA+B+AuAOCcBwEEGWM3ApgT2e1ZAHsxwoMRgjBD0zgOne7F4uf24Xi3H7UVMp68Yzom15RD0zjeP92LZVtbjec2LWzCv+35AG+0dcTsOxwf3snmauf8Vse7JAF3/PT3QxqTIEYSg4MKDnf14964vwn1lZ6MA5Jil2kuBtAJ4GnG2AHG2P9hjHkA1HDOT0b2OQWgJm8zJIgCpqs/aHw4A8Dxbj8WP7cPXf1BdPQFjEBEf+7era1obqpL2Dffc83k+GNdA0MekyBGEl3+oBGIAOf/JnT5M/99KerMCMLznwbgG5zz3zHGfoSwJGPAOeeMMdMqcIyxJQCWAMCECRNyPVeCSItc3Z/RUgUAVHldxh8XIPwHJqioUDQes11/zic7EvbNNmZySlBRTefjD6k40T2QUmKxOr7MKSZsG+o1pSsjZSo75RO792e81FftdUGSiv178MjE6m+CotkutGpJsQcjxwEc55z/LvJ4B8LByGnG2AWc85OMsQsAdJgdzDl/AsATADB9+vTMX02CyCK5uD/NpIr18xvx6O5DONDeAwCorZDhlEQwVUNthRzzx6e2QkaPPxTz2CmJCefJ9hyfvGM6Kj1O0/kc6ejD3c+8k1JicUqi6fEDwdjAY6jXlK6MlKnslG/s3J+KoiVIfS0LmzClppwCkiLEITDT3yFHFu7Xor4bOOenALQzxiZHNs0F0AbgFQB3RrbdCeDlPEyPIAoOM6lixY6DuH9uPQDEfPCXOQVsXDANtRWy8dymhU3Y2dqesG+u57j4uX0AgPXzG2Pms35+IzbsORyzn5XEUulx4sk7pscc/+Qd0zGxsixh21CuKV0ZKVPZqRgwk/qWbW1FR18gzzMjhoIkCqa/g5KYeShR7JkRAPgGgOcjTpqjAO5GOMjazhi7B8AxALfkcX4EkTfiZQBN00zTrJOqvXhr5RfglERUyA509QcxEFSgahqe+9pVAABV49j9vyfxvRs+jQfnfRoiA2RndrMigLWcMhhS8ejuQ1g9rwE+2YHqche+vf2PRkZH3y+oqJaumZpRLmxbMgMqB9wOAWM9LgDAruWzM5ZKrOZtJfkEFRVVXpdxPT3+EFr2HsmJ7JUvQqr5/aaoWp5mRGSCP6Ri1/4TePquz0AUGFSN48lfH8XXr/lUxmMXfTDCOf8DgOkmT80d7rkQRCFhJgNsXtSEaxuq8UbbeeWytkKG7BBRVe4yPWZdcyN+8HpYxrm2oRrXNNRg6ZbWnEkLVnKKJAro7Atg6ZZWAMDmRU3ojPuGXVshwyEJtl0zYz0uCAJDVbkrZ/O2knxkp4gHrpuMFTsOxkhmuQjw8oVDFCzfS6L4kB0ibpo2Hnc/807sPevI/J6lO4IgShQzGWDpllY8eH2DpSxhdszKnQexbM4k1FbIePD6BiMQ0Z/PtrRgJadUe10x23e2tqNlYVPCfpLA8uKasZq3leSjaNwIRPQ5rdhxMCuLAQuFaq8r4T1qWdiEam/mwR8x/CiqZn7PZiHTVfSZEYIgzLGSDRhjeGn5LIQULUaWSeauuWxcuSFlpCNFDNVdMsotYfvSmRAZIAiCcdzkmvIYSaVCdiRILCfP+XPqmrG6JrP5JbvekGIuYYSU0pEwJEnAlJpybF86E4qqQSI3TVET0riptBgiNw1BEFZYyQYfdvRh3Gg3JteUA4Atd43slFBV7kJnb8C2FJELd4mZpBL/OJeumVRzTEfySVfWKVYkScCFPjnf0yCygFsSTKVFdxaCSwpPCaJEMZMN1jWH3Se6RJGOu8ZqTCspIl/ukly6ZrLpgElX1iGIfKNxmMo02VAWKTNCECWKLhtsWzIDx7v96PGHjIWoAAyJIpW7JlpqSEeKSNctkq4ElOq64+cInHfNyE4RisZx8pw/LQdNOnNMJVGlK+sQRL4Jqpr57zStGSEIIhmCwOCURHzn53+0lAPMpALdXWM1ph0pIl23SDZlC6s5WjmG7DqC7M7R7jmy5eQhiOGAZBqCIIZMMjkgl1JBum6R4ZItMpFa7M5xJBQ0I0YeHOYyTTb8X5QZIYgSJ5UcYCVpdPYGMpIP0nWLDJdskYkcFD/HeLmnQnag2x/CQFDJiuREEIVEwOJ3OpAFBxgFIwQxAkgmB8Q/l62eKUORXYZDtshUDtLnaPY6tSxswoY9H6C5qW5EOGWIkYXTooidMwtF7EimIQgihly7WvLtFsnWvMxep2VbW9HcVIeWvUewrrmx4K6dIDJBYOb9obKRvKTMCEGMANIpPpZrV0v8edMtjJYpgsBQX+XF9qUzEVI1o5R1tpw1PtmBA+09+MHr4T46l40rh+yUyClDFD2Dioa+wRC2LZkBReOQBIa2v5zDIMk0BEGkIl3ZZThcLUOdWzbQNI7DnX1Y/Nw+VHldCe6ATJ01Pf4QAOBAew/WvNqGXctnk2OGKAlGyyLG+cpw6xO/NX5fNi1swmiZetMQBJGCdGWX4ZRX8uE6iT7nsjmTEtwBmThrWhY2YWdru/GYpBmilOgPaLh3a2xvqnu3tqI/QJkRgiBSkEp2MZNJhqsYVzaLiKVzTr1wU321N2vOGt1N88hNjXjohvR68VDRM6IYUDRu+vuSjeaOFIwQply06jXb+3689voczoTIlGSySzKZZDikBau5qRqHpnHjgzmbck50MbbV8xqy4qyJxu7rlg+JiiAywSEw098XRxbuV5JpCKLESSa75Ls4V6XHic2LYlvMr2tuxMOvtcXMIZvzjC7Glk/XS75fe4JIF0kUTN00UhasvZQZIYgSJD79X1/lNZVdrGQSf0jFie6BnEsHgsAw1uOM6XWh98956IbzUslQpCarOUcXY0vmesm2hBI/nqaZF5AKKmpJyTeldC0jHX9IxaO7D8X8vj66+xB+eNuVGY9NwQhBlBjppP+tZJIjHX24+5l3hkU6EAQBa15tSyqVDFVqsuMWMnO9ZFtCMRtv86ImXNtQjTfaOmKuySEJJSPfkBRVWkgCQ2dfAEu3tBrbaitkSCTTEAQRTzrpfzMJZ/38RmzYczjlsdnCjnsnm1KTnfNlW0IxG2/pllY8eH1DwjwkgZWMfENSVGnhcQnYtDBWVt20sAkeF8k0BEHEES1pTK3zYdmcSfDJDiP9n6yNPQDc98IBHGjvMfbJdU8VO8XRku2TbpE2O+fLVuE3XaKw6lUjCgy7ls+GpmlQOcA5hz8YdvtE71+sfW2inUsxLeeL8FoI4JxfxamegYSiZ6PcEnxlmY1NwQhBlBi6DFHldeG7X5yMlTuTF/SKdoR09gbQ2ReIGW84eqrY6UljtU8ueuBko/BbtESRzLVT6XEmSBnr5zfi0d2HjKCwWPvaRDuXoq9NdhbftRCAWxLgdTtiip6tn98It0S9aQiCiEOXIe6fW28EIoC9FHmh9pNJRi7mnI0xoyWKZK4dMyljxY6DuH9ufdauJ19EO5eA89eWjboUxPDDAdP3MxvvZtFnRhhjHwPoBaACUDjn0xljYwBsA3ARgI8B3MI5787XHAliuKn0OlHmFLF6XgNa9h4xvmEnS/frksIot4TtS2dCZOHFpfqHYGdvoOAcEfqcx5Q5sH3pTHDOszI/u311khEt9SRz7VhJQpOqvXhr5RcK6vVOl5BFy/lQFnqZEMNPQNEsZDeqwKrzBc75majHqwDs4ZyvZYytijxemZ+pEcTwYeZeWNfcaNhlrdL9yVwPAArSEWE9Zzkr87IjHSXDjmvHbD8gnA2RHWLR97RxSOYt5x1ZSOsTw4/sMJfd3A7qTWPFjQCejfz/WQB/l8e5EMSwYZbyX7nzIJbNmZQ03Z/M9VCojohCnZeOXamnGKUxu0gCMy+SVYRZHiK3slspZEY4gDcYYxzAZs75EwBqOOcnI8+fAlBjdiBjbAmAJQAwYcKE4ZgrQdhmKPenVcr/snFhycEq3Z/KPZINZ0m2yZbjJVfYlXqyIQnlAzv3pz9oXiTrx7dPBTzDOVsiG4RUC9lNJZkGAD7LOT/BGKsG8CZj7P3oJznnPBKoJBAJXJ4AgOnTp9OKKqKgGMr9aZnyd0qoKndBUTSc+mQQIVWDQxRQ7XVBkgQ4JRHXNlSjuakOPtmBkKrBJYlQOYckCKbFuYbi7khVjdNutU5N42CM4dqGatw9+2KMG+WGyjnO9AULyqlhJfWYXWexSTJ27k+nJJoWySpGZxARznRF/53o8Yews7U9K5muog9GOOcnIv92MMZ2AbgKwGnG2AWc85OMsQsAdCQdhCBKBD3lH7+OotLjhKJoeP90L5ZFWoDrLe+n1JSjQnbg/rmXxjy3fn4jvvmzP6CzL4CWhU0AgDfaOoYsI6Sqxmm3Wqe+37/vb8d3vzgZXX1BLPrp788fs2g6fHLhZhZGUlVSn1vCpoVNRtt5vUiWz130Hz0jkkrZiW/MvTTh/ayUM5cUGefFmxBgjHkACJzz3sj/3wTwrwDmAuiKWsA6hnP+QLKxpk+fzvft25f7SeeJdLrwpssI6Nqb90+IdO5Pq+zCX3r8uGXzbxKyJtuXzoRDFHDTxrcSnls9rwFLt7Qa+2XiVunsDZieQ1/Qmer5+HFWz2uAUxSw+uV3Ux5TSNi9zjQo2PvzLz1+fO+VdxO+SX/vy5fjQp+ch5kSmXCie8CoMaJTWyFj25IZGF9hWfXM1v1Z7OFpDYBdjDEgfC0vcM53M8beAbCdMXYPgGMAbsnjHAliWLGSBqz0XgYOv0WFUJ/sMP7POU/2ByclqdZ42K3WqY8TPTezMXPd6C6ZhKTv55AESAKDP6hCdopQtHCF1UJe65JNQqqGzt7YBcWdvUEoWVhjQAw/isZN790Rv4CVc34UwBUm27sQzo4QBBHBISbaLK9tqMbZ/hA6egOma016/CHj/6rGE8rJp0OqqqZ2q3Xq4/T4Q3CaXJM+14+7+nFHtHyT5UZ3ySSk+Gqqu/afwE3TxmPFjoOW1VhL0e6aSysoMfxY/b45RarAShCETaq9roQmV//0tw1YurUVG/YcTqgQunHBNLTsPWLUKnn4tbaMbLOpLKx2bYP6ODtb21HhcSRYRx+7+Qo8/FobjnUN5LTRndl4VtVUF3/uEuPazKqxlrLd1ew9JYoTgcHUqp2NW7eoMyMEQSQSLRPo0kBI0eCURIz3ufCzxTPwlx4/evwhcITTrse7/UaFUJ/sQHW5C6LIsOpLUxBSNQgMuOezlyCoqFAUDWf9QaiaBq6FgwhRYJCdYtKFo1YWViC8jsJKvoiv1qmP88hNjdA0DRzAlq9dBZVznDo3iLW/eB8H2ntwz2cvSRgrWgrRNI4z/QEMhlSILHb+8ZKMXRux1X6iwEyrsdZXe3G4ow+P7j6EH311Knzy0DNPhUguraDE8DOoaNi1/wSevuszEAUGVeN48tdH8fVrPpXx2BSMEEQJES0TVHldCSnyzYuaoGoc3/n5H3G8249ffufzRtr1QHuPsVh1zY2XAwA27DmM734xdoyWhU34jz8cxzWXjTPG0b8h1Yxy46JKT9KAJHo9i91mcsnG6ewNYNFPExfmDgRjA4XosazklJpRbkyoKMPhzr6Y5174+6ttzc1KilI1blqNNXqB8JGOPvQHlJJy1ZhJg7UVMhxZSOsTw49bEnDTtPG4+5l3qFEeQRDWRMsEy+ZMSkiRL93SikqP00i1nvMH8fgtVySkXevGyJhYWWbabG/Z1lbMnz7BCET07St2HMSxroG0pBC7zeSSYSX/TKwssxzLSk451jWAjr5AwnMPv9aGzYuaUs7NbC7r5zfiyV8fNU1vR8tgG/YcLqgKstnC7LqJ4kTj5rJbNvoeUmaEIEqIaJmgutxlufLdqIpZ5sS3t/0Ra7/yVxg32g2RMZz6ZBDlLgmVHheckoDHbr7CcLYcaO9JkB2ixy5zioZ0Ycd9Et9M7uUD4RSwUxLgEAVURbramklO0YGFWXM/TePYvnRmTIE3/fxWckqZU4RiIi280daB73/50yntzfFSlO6m+eZf10N2inhp+SyEFA0OSQDXOFZ9aQp6/CGjd5A+t1LBH1LR3tWPF5fMgBqR894+3InxZOstSoKqRaM8qsBKEEQ0ukxQ5XVhtOywlAw6+wJo2XsEj91yBTr7Alj41O9j9nnlvtkJUoXecK+zL5AgO+jHDQTDgYdd90m0rDG1zocbp8amgFsWNmHDng/Q2RtMkJye+9pVCCiaZXO/+PlHn99KThkIqpAspIWDJz7BmlfbUjbjM7VWm5Q+7+wNxGSX9POUUnXSUW4Rl4334bZIbQq9SFa5u3SucSThlgRzdxTJNARBRKPLBPfPrcfaX7xn6pDpHQxhXXOj5T6bFzVB0bhpw73759ajZWETduz7Mx67OVHemVhZhspINsOO+yRa1lg2Z5KpJNTcVGcqOR3rGhhycz8rOWViZRmqva6E59Y1hyWVTF05Vteun6dUGuTpDAQ1o1onEH4f7t3aioEgLWAtRkimIQjCFrpM4HGJeKOtA529wZiUKgPgD2n4weuHsP7mRtN9xnqcCCnmLohJVeHFqXfOvgSSyLB9yQxTN41d90m0rDFgUXhtUpUHAmNYPa/BkIoAoMwpJj1Hsuf08760fBYGQxpEhpj563PyBxW8d6o3RkZJVaDMbnG0Ym2Qlw65LJJFDD9BC3cUyTQEQSQgCAzuiAyhO2QAGC6ZoKrhQHsPTp0bNN3npeWz4BTMpYojnf24+5l3UhYRS1XgLH6+4XLwMD2m/azfOKcuFR1o78FAUE16jlTnFwSG6nK35Wuoz2nNq222pZR0+85YVcstFRwCM3fTlFDANZLI5ftJMg1BlChWLpmdre0AAJckmjodJIFZyhgb9hwGkLqI2FAkCDvnXLnzIJbNmYTairDbx+oc2ZJA0h3Hrjw1UnA6BNN7zOmgj55iRBLN308pC1ZtyowQRAniD6n4f/7z/QSXjFsS0NxUh3s+ewmqR7nwDy/+IUaieXT3Ifz49qnwyUDNKBe2LZkBlQMiA+574YAhVQDJ5YqhSBDxxwDm57xsXHgfPSCwOkc2JJB0ryOVPJXtfjmFTiCknXduxd1jRPHhD6mm7+cPb7sy47EpGCGIEsQhCqYumafv+kxMF97OvoAh0ej7OCQhQWp44e+vRmdfIOYcqZwfQ5Eg4ouZmZ1Tdkox41qdI1sSSDrjJJOn0pVwSgGHJFjeY0Tx4RCY+ftJMg1BEGZUe11oietDs3HBNDz566PGh6CZa+TJO6ZDEtiQi35lk2J0mySb80iUcCSBWUqBRPHhlCxktywEl5QZIYgSRJIETKkpx/alM6GoGiRRQJlTwDf/uh4rpCmGPGAmQZw85zct+rXmxsuH1fmRL7fJUKUU/Ti9AJtTZAiqHJyfH8+Ow6iU8AdV014m3/zretPaK0RhE1ByJ7tRMEIQJYokCbgwrtKlryx2HzMJwkpqEARh2J0fw+02GaqUYnacXrDtjbYOQ+qy6zAqFWSnaNrLRHaW7jWXMrr8myDTZGEBK8k0BEHEUIzySLYYqpRidpxesE1/nA+pK98oGjctkkV1RoqXXPUaoswIQRAxDEUe0TSOM30B+EMqRIHBKQoYU+aEFKUlW+0jCMyQMRhjMfKG7BShqDzpuPrY6Ugr0fvr/WP8QRUqNy/SlUpKsZJgfLLDeGxX6iolx01I0fDTO5vgcTmgaBySwNAfCCGkUAXWYsQfMpfd7rvmUxmPTcEIQRAJpCOPaBrHoVO9WLxlX0wq/pNyFy4a44EkCUn3ERjDHT/9PY53+3FtQzXuu6Yey5/fjyqvy7QPRvS4xvnTkFbM9l8/vxGP7j6E++fWD0lKsZK2evyhmMeppK5Sc9z4ZAFnB4CvxfWmGS9TUr4YkR3mspvbkbnsRndEAXHRqtds/xBEodDVHzSCDOB8Kr79rB8dEWtusn2OdQ0Y25ub6rD8+f1hmcOkH038uMbYaUgrZvuv2BEuprZhz+GENLQdKcVM2mpZ2GQUmLM7Tqk5bnr85r1pevyUGSlGFFUzl92oHDxBEENhKFKA2TEAMBgy7ylT5hShqBpOdA9AtehRUhZZyHhLUy0Wf+4SOCTB6EHjkx1Jx9XnMxBUEvrWJJNWkkkqB9p78OjuQ9i2ZAYA2H5tzKStCtmBR25qxEM32H+NS81xQ71pSouQxlHldcW4aVr2HkEoC+8nBSMEMcIYihRgdYyvTILGzfvADARVcADf/48/YdWXLrPcp9LrxMKZE2NSv+uaGxFSNdNjOAC3Q0yYT3TfmmTSSipJpbMvAKckZlSwTSfdMdLp6VMMSBa9TKjOSHHilgRT6dSdhTojBSPTMMZqGGNPMcZ+EXncwBi7x+axImPsAGPs1cjjixljv2OMfcgY28YYK93l6gSRJkORAqyOUVTgkdfa8NjN5n1wHnmtDc1NdVj7i/ewrjlW/ti4YBrqxsio9DgNaUYfe+XOgxAtCmaN97mhajxhPtF9a5JJIlY9cFr2Hsm7w6XUnEwel4BNccX3Ni1sgsdVMB89RFowU5kGyDy4LKTMyDMAngbwz5HHHwDYBuApG8d+E8B7AEZFHq8D8Djn/EXGWAuAewBsyupsCaJIGYoUEH3M1Dofls2ZBJ/sgMY53mjrQGdvMKYPjuwUjefu+ewlxj7R6d0qrxMOUUBQ1RLSvgfae3ChT8ZfevxY+5W/gkMUjAJL/3JDA8Z4nKbXEN23xirLEy+pCIxBYMCPvjoVboeAsR7XsCwWtZLK8lHoLVec86t470QPXlwyA6rGIQoMbx/uxCj32ISaN0Tho2iahexWWmtGxnLOtzPG/hEAOOcKYyylUMoYqwVwPYBHAHybMcYAXAPg9sguzwL4HigYIQgAQ5MC9GOqvC5894uTsXJn+NvRf33786itkHGgvcfog1NbIWPNjZfDITJD/tD30Ysl6fvUjZERCGlY82pbjNzy7NsfgbHYb2H6cT0DIdSMcpteQ3zfGiuESGdiM+lprCf3RdZSSWXDXVwuV0gCw4ZfHcEDL71rbKutkLGtviqPsyKGikMUTH/vSq3oWT9jrBIABwDG2AwA52wc90MADwDQQ7NKAD2ccyXy+DiA8VmeK0EULUORAvRj7p9bbwQiAPDEfx/BxgXTEiSPDXsOGzLLztb2BIlmXXN4n/azfiyNc1us3HkQ/3x9A17efzzhuPXzGzGxssyyr046ckY+nSul5pqxwu0QEu6PjQumwe0opI8ewi6cc1PplPPSWsD6bQCvAJjEGHsLQBWA+ckOYIzNA9DBOW9ljM1J94SMsSUAlgDAhAkT0p4wQeSSXN2f6UgBiqKhoy+AkKrBJzvgK5NivhVtbz0OANi2ZAaUSBr+Gy8cwIH2HnhdEs75Q3jguilwiAJ+vmwm/tw1gB5/yFhoWuYUjdX51eUueF0SBkNh6eS6vxoHSRTw/N9fDVFgEAUGh8AwJiKjpLqGVI6hoKKaOgNSOVfScSJFv34OUUC11wVJEkrCNWPn/uwLqBgIhIz7QxIY2s/2oy/gQKV3OGdLZINBi940P7ztyozHLphghHO+nzH2eQCTEV4Nc4hzHkpx2GwAX2aM/S0AN8JrRn4EwMcYkyLZkVoAJyzO+QSAJwBg+vTp5DUjCopc3p92pABF0fD+6V4si2Qu9NoZ1zZU4422DmO/t492YYU0BePLXTjRPYDOvgCm1vmgcWDVS/9rHPuT26fhqf85GnOswFjC6vx1zY34t18exn3X1OPHrx8yerusn9+IqnIXxkRklGTXYMcxJDtFU2dAsr4p6TiRrF6/KTXlJeGasXN/+mQRnww6cWtc0TOfXDzXSZzHJZn3pnGVmJvmKwC+jHAwcimAGxhjcxlj1VbHcM7/kXNeyzm/CMBtAH7JOV8A4Fc4n1W5E8DLOZ08QZQgHX0B44MUON9v5Z+vb7CUR6q9Lmxa2IT759bj6y/EOmS+/sL+hGPHjXYnrM5fufOgUfwsureLXvDMjpRhRwYZSt+UdOQVq9evoy9Qcq4ZK/oC5kXP+gJU9KwYYTDvTZON5dUFkxlB2PEyE+FAAgDmAGgFcDFj7F8551vSGGslgBcZYw8DOAB7jhyCIKIIqeYr5xmAXctng4FD1ThCGkd79wBkh4gxZU7UlLswyi2ZHgsAP1t8NTQeXgxntTpfL3gW3dtFL3hmR8qwI4OEFPNzhxQNZ/sDRq8at0M0HDbpyCtWr5+iaiXnmrGCip6VFoOKZtqb5usl1ptGAnAZ5/w0EK47AuA5AFcD+DWApMEI53wvgL2R/x8FcFUO50oQJY/VynlJFFAhO/Dx2X509gaM7MK1DdW4f+6lWLa1FavnNZgee7SzH26HgEehM7Z+AAAgAElEQVR3H0JnXwA/WzzDsgCZWW+XgaAKVePQNJ70g9uODGK1j8CAQ6d6Y+QbXYpJR15J9voB6fX/KVao6Flp4ZYE8940pSTTAKjTA5EIHZFtZwGkWjtCEESWqfa60BJXsKplYROqvS509AXQftYfI3M0N9UZskTL3iOWDhq9D8zxbj9OnRtMSPuuaw47cDYumBbT22X9/EZUeBx4+LW2lFKNHRnEbJ/Ni5pwLO66oqWYdOSVZK/fSEF2mhc9k52F9NFD2GdkFD3bG6mg+vPI4+bINg+AnvxNiyBKGyt3iCQJmFJTju1LZ0JRNUhRbpCQqqHMKcZ849WlFb0o2ii3hJ8tnoEzfQF09AYMB42+LwBonBur86PdNP9yw6chMuChGz6Nh//ucoTUsCSkccAnOy2lmuhrqRnlwkvLZyGkaKYyiJlUomka+gbNe+0EFTUteSX69WMIz50D6PaHjGP0+WqaBpWHrZOlJNn0DloXPRvjyffsiHQZKUXPvg7gKwA+G3m8D0AN57wfwBfyNiuCKGFSuUMkScCFPjnhOIcoYCCoxqTge/whXNtQjTtnXWzUIokuta4HItHyy0BQNV2dv+bGy3H3M+/g2oZq3HdNvVEuvrZCxqYF0+BxJcoiQ+m5Ey+VdPYGEq5Ln5MuxaQjr0iSgHGj3Kbzqq/y4nBnHx5/81DCa5Zq3sWC7BBRV+nBbVFumvXzGyFnoeU8MfxIgoX0KJSQTMPDVVOOAlAA3IRwAPJeXidFECXOUItvVXtdqBsjx0gsO1vb8c/XN8QURdPTuPfPrQeQ2AemboyMx29J7GuzYc9hADBcNTFujOf3YyCY+E0sG4XEKj1OTKwsS5COMnG6WM2roy+Axc/tQ3NTXcJrVioF0HLZcp7IB+ZFzyK1SjMi75kRxtilAL4a+TmDcD8axjkv+mzIRatey/cUCCIpQy38JUkCJlaUodwVlmJUjaM/qECzcE9cUuXB3u/OgSAAnAP/ckNYlmEMWPHz943zV5e78O3tf4yRc6wcKWbXYiWv2C1UJggMF1V64CtzYNuSGVB5uIroGNlperymcZzpD2AwpBo9eXxyYnE1q2uo8rpwabUXj918RUxfnmIrgGZFLlvOE8PPoKKhvas/QXYzy56mS96DEQDvA/i/AOZxzj8EAMbYt/I7JYIYGQyl8BcQlkQ+PNOPU+cGsfrld42eNR1KwDSN+/6pXqx5tc3oO3P37IshO0UMhrQYmWbzoiZ09gWMY3VXjZUjJRorp4vsFNOSb4RIlVd4zl9rMpklevv6+Y2oGeXGRZUeY2yreTnEcDv2RT/9fUzBtx+8HnYaFVMBNCty2XKeGH7K3SIuG++Lkd02LWxCuTvze7UQ7oivADgJ4FeMsScZY3ORjaW5BEGkZCiFv4Dz0sOGPYfx2M1XGD1rNuw5bOqiadl7JKagmX6OeMeJ7qKxepzMkWLldFE0npF8k0pmiX/tjnUNxIxtNS+nI9GZsHJnWNIqlQJoGofp/UWJkeLEHzQvYuc3kU3TJe+ZEc75vwP494hr5kYA/wCgmjG2CcAuzvkbeZ0gQRQZ0Q4NjQMhTYPEGCRRQEAJ933R5QSrwl+BkIYT3QNG0a8xshPd/hCCigo5Unhs04JpcDtEqJqGmtFuHO/243i3Hz94/ZCl7BJd0GwwpEHwMEyu9uLnS2cipGoQBQbZKRhpYCnqsaZxOCQBVZ6woyf6WvV5VY9yJsgrf/nEn7RQmZ0eNlYyi9n2+MJsVg6ck+fM5zWpygOvO+9/mrNC0OI1CtKakaIkl0XsCuaOj7hmXgDwAmOsAsDNCFdSpWDEhEJaj5LuXD5ee32OZkLoksLjbx7CPZ+9BN/5+R9j0uN6sTFdTvC6JVMJIaRquCNKPmhZ2IQNez5AZ28QD1w3GU+/9RHunHUx7o0sLn36rs8Y4xxo78HSLa2GK0YPRPSxdenlSEcfFFWDQ2ToHghh+fP7UeV1mab19Xk/ecd01JS7Y6518XP7TI977mtXoasviFPnBi3dMXYcOFYyi2RR1GwgqCZILGYOHKtx34tIWqXgqMlly3li+MllEbuCvCM4592c8yc453PzPReCKCZ0SaG5qc4IRIDz6XG92JguJ0gCS5AQNi6YhrW/eC/m2GVbW8NFzeZMwoodBxMcIBv2HE6QUx67+QqM8ThMC5r95PZp2LDnMI51DSCgcMMxo49vNe9oeSVaPjE77ljXgCElxUtHugxix4FjJbNUe10J29fPb8TEyjJbEovZuNGSVik4akRm3stELN74akTjcZkXsfO4Mg8lCiYzQhBE5uiSgpULpb7ai82LmtCy9wjKnCL8QTVGQgCAs/3BmM66+rFTxpVDYAxVXlfC+Afae8CAGNfE2l+8DwDY8rWrAAYoKsdgSEVzUx0EFj6mzClCYOf71ljNWy+SFi2vRMsnZsfpRdnipaPaChkXjJYte81UeV0IKipOn/MbhcisCqhNrinHS8tnYTCkQWQwddNYES3f+IMK3jvVG1MYrhQcNblsOU8MP+f81kXsfGWZjU3BCEGUEHrq38qFcrijD2tebcP6+Y0QGINTEmMkhM7eAM70BZM6YtbPb0RI1RL2OdMXxJpX2xKO+7hrAEFVMxwztRUyVs9rABAueqZvO97tt5y3XiQtuvhYtMxhdlx08bJo6WjX8tmWEszUOh8euG4yvv8ff7JViEwQGKojstFQ0F/7zl6YvnbF7qiRBGZa1I560xQnksCw4VdH8MBL7xrbaitkbKuvynjsgpRpCIIYGnrqf2drOx67+QpLCWDFjoMYN9qdICdYFf2KP9YliQnSxxiPAz+89cqElPz4CndMj5nHb7nCKHo2sbIMXpdoSDwte4+YpvX1/aNdJtEyh9lxEyvL0u5Pc//celMZKteySTo9b4oJn2ye1vfJ9NFTjHjdoun76c2CtZeFC58S06dP5/v27cvqmIW0yLSQKMIFrHn/GpfO/RnvpgmqGt4/1RtTkh0A/u8Dc+ByiAnSg6Zx9PiDGAyqCGnc9Nhfr5gDlyRA0bjhepFEAZxzw8EjMAaHwCAKDIOKBk0LO3MkkcEfWeRZITtw8hM//m3Ph1j8uUsgRvbv7A2gutwFSRQgMiCgcrgdAsZ6XDGZiXg3jaLxmOsBkLLYWfQYKuf43KN7sW3JDNz6xG8TXtu3Vn4B4ysyzEdbED0PxhhEBgiCYKdPTcHen8e6+uFxCggoHErkPnFJDP1BDRMrqTlNsXGiewBvHe7ErPqqGJlmdn1Vst8LW/cnyTQEUWKY9VsxkwBCKsdXn3zbVIbwyU4c+qQXp84Nmh7rEAVUlZv3XNHHSOZUGeM5//ypc4N4+2gXtrcejznHruWzU/aAsdMnJp0xOnsDSWWuXMomgsBQ6XGm3V+nkHGKAv5u428SXsefL52Zx1kRQ0V2WvQaSlEk0Q6UGYlAmZHCpQAyKXn/FMjk/jQLCn5y+zT85FeHYxaqRgcAnb0B3LTxLaOyanzju0vHeaFpDDdtfCvhgyZ+jFTPm50jXx/Amsbx3qlP8KP/+iBhzcjmRU24bNyonM4p1WtmQcHen6fP+XH0TH+CVfuSsR7UjM68hDgxvHT0DuIrG99OuD9fWj4r2dopyowQxEhDUTR09AUQUjU4RAHV3nCBsMk15di2ZIax2FNgMHXMxDtVrIqY/fj2qcYxqcZI9xzRbhcr7PaaSXd/QWAY63GiuakOo9wSnr7rM1A1DaIgwCUJOP3JIJwOhsGgZuu86c411WtWbJCbprQIKRpubarFjdNqoXEOgTG8vP84QkoJVGAlCCI7KIqG90/3YlmkXLNerGxKTTkkSYBTEo3aI5sXNSWVIaJdJtFOlNXzGmL6ptgdI51zRLtdzLBTqCyT/QVBMKSpqXU+08xQdBG2ZBmcdM9t9ZqpGoem8aKTashNU1p4XQLmXFaD25+M7U3jzUKdEVrSTBAlQkdfwAhEgPPFyjoijedSuU+snCr683rBMn2/VA6QTJ+3wk6hskz2j57XsjmTElw1VkXYsnVuPVDUX5N1zY14+LW2oiyA5nWbu2m8bvroKUb6Aua9afoClBkhiBGPLgOEVA2r5zXEOF/0HipAYo8U2SnipeWzwDVuFPfq6g/GFPTS99XdHY/c1BgjM5j1XNEXr3b1BzGmzIHtS2eCcx7jcOnsDSCoqPDJDvz78llhtw3ncEsievxBhBTNmFO8tGElZfiDCjp7Ybu3jJX0EX3tA0HF9NjqyPqNVBLKUM491uOMkTX0QmgP3VB8Uk3PgIpqrwPblsww3DSSEN5OS0aKjxHRm4YgiPQxkwH0NvQH2nsS+oDEu09SyQhDcbNYjxn+9Il/buOCafjxL8OLafU6JA5JwH0vHDCdU7o9XVLJRcmu6y89icXdaitkjJYdmFrni5GszBjauYWSKYBW4RFxrCtgfJvWMyMTK5PfV0RhksveNOSmiWDHrUDumPyQjpsmR0378i5wW92fVu6L1fMajGqpl47zotJjvtJ9iO6NpCQbE4DlfKMrtK658XLc/cw7pnOyE4BFzz/ddRvRmK3DWdfciGff/ghfvWoixo12Z3XNyBCPKdj780T3AG6N2EB1aitkbFsyI2f1WojccW5gEH/uTgwuJ1S4MLpsBLtpGGNuAL8G4EL4WnZwzh9ijF0M4EUAlQBaASzinBef4EoQKbCSAaaMKzcWWv749qmARX2pobo3kjlELGWUkArOzdO8eu8Z/XFZpG7B1Dofls2ZBJ/sQEBRcbY/AJ/sxOSacrxy32wMBFVonCOkcvzLDQ3o6A2gZe+RmPnHS05mcpKV00UQGKq8Tmz52lVQOcepc4NG0PPgvE+j1pfc9SMIDPVVXmxfOhOKqkGKOJxSHWM132JD0TiqvK4Y2all75GspPWJ4acvoJn2phlTVoXRI7w3TQDANZzzPsaYA8D/MMZ+AeDbAB7nnL/IGGsBcA+ATfmcKEHkAodk3qL9aGc/nJKAqnJn1mWEVN/crcY80tGHoElPG73IWPTjgaBq6WSpGeXGhIoynP4kgMffPJRQD8SsCFN6cpJ10bZ1zY3GHGWHaMvWe7izL+2sjB2JrBhwSwIeuG5yQp0Rt0QLWIsRt1MwLXrmdo5wNw0P0xd56Ij8cADXANgR2f4sgL/Lw/QIIudIAjPtI7Nhz2Gs3HkQD17fkNSdMhRHSyqHiNmY6+eH59Sy90hCT5uNC6Yl9K6p8Dhw/9x6UyfLsa4BdPQFsPi5faY9ZFbsOGjrm3eq6zB7fuXOg7h/br3tvjHpumlKDQ4YgQhw/v2hvEhxEgxx0/czGKIFrGCMiQhLMZ8C8BMARwD0cM6VyC7HAYy3OHYJgCUAMGHChNxPliDSwM796Q+qeHT3IWz52lXo6A3EuC8AQBRY1iWBVNJO/JgAcN8LB4w56QXOLhtXDkkU4BQZvvfly/HQDRwOSYAkMIQUDRVlTtPzlDlFhFTNkHfM9rFThMluUbb45ydVe1PKM3bPUczYuT8DimZ6/YEsFMkihp+gav5+hlSy9oJzrgK4kjHmA7ALwJQ0jn0CwBNAeAFWbmZIEEPDzv3plER09gXwQUefLQeG1RqJZJJAfFXXMpeAp+/6DMqcorEGIN5VEj3m2f4A7p9bH7P/mlfbLBfJ6nOUBG4q6VR6XRAjq/oz6SGTTlG26OftyDN2z2F17cWwVsTO/ZlL9wUx/DhEAdc2VKO5qc5YA7SztR2SmLnIUvTBiA7nvIcx9isAMwH4GGNSJDtSC+BEfmdHELlBl0Qef/MQ1jU3JvR3iZYShuLsMHOTbFrYhJ/9/phhxdXXcZjJFprGcfqTAFa//G7Cug+r/fU5VnldWD+/MWa9wcYF0/Do7vfQ2RvE+vmNePqtj1Jed6rXLv71iC/KZvW8HdIZIxPXT6FSKTuxaWFTgvuiUrb/GhKFQ5XHiW/MvTTh/axK43fCiqK29jLGqgCEIoGIDOANAOsA3AlgZ9QC1oOc843JxiJrb+FC1t7k96f+bVrTrAuFAUOz8f6lx49bNid2XY234lo1yrI6p939p9b5cP/celw81gNJZPjX//iT0VNHf27KOC84mOV1JyNVJiIbmQq7Y2Rgsy7Y+/NE9wC+/x9/Svgm/dANnyZrbxGSy0aOxZ4ZuQDAs5F1IwKA7ZzzVxljbQBeZIw9DOAAgKfyOUmCyCV2nRdm6xeqvC4EFRUnugfglERUyA50+0PGB6dioRHHW3H1NRrRH7xupwB/0HzNhNWajvg5Hmjvwd3PvINffufzULXY5n76c79Z9YWU125FqtfO6vl0gpRM3p9iX1+iaBydvbGLdTt7g2TtLVJyeY8WdTDCOT8IYKrJ9qMArhr+GRFE4RK/fmFqnQ8PXDfZKEpVWxFurLdhzweGBPP8319ty4rrlMQEieWB6yZjMGRu5bVaM2G1xuJwRx+cYqKN+dqGanT1h2JkpFxLG7mSU4Zisy50ZAtrr0zW3qLEqpSAIwvvJ90RBDFCiLfc3j+3PsGmt2xrK5qb6ozHj7zWhs1xjc7irbj6GohoG+uyOZOwYsdBbNhzOMHKm2zdhVWDvpa9R7Bhz2FsXDAt5rlVX7osoTlgrq2zubLrDrVxYCGjcHNrr0KJkaLErJTA+vmNWVmQXNSZEYIgErGSEOItt6qNaqhvtHXg+1/+dEwFza2/OYbmpjo8eH0DZKdkjB+dwtUtt8e7/YaV1yc7ML5CxoWj5aTrMuqrvNi1fDb8QQXvneqNsSozIGYu/RYyUFBRc+ZMGUqq2s5cSqnyqk4oh1ZQYvjxB1Xs2n8CT9/1GYgCg6pxPPnro/jmX9dbVnm2CwUjBFFCpJIQ9PULmsZxvHvAlgTDwRJsw28f7Uro/6Jq56240ZbbA+09WLqlFbUVMrYvnZkQiFjNtwtIOO+ZvqCxbWqdD4/feqXpNXAkNuTLlnwzFLuu3bmUSuVVHbL2lhZup4Cbpo3H3c+8QxVYCYKwxq6E0NUfxMOvtSVIKJsWNiVIMNVeV0r5IH68lr1HEtK5mxY2odrrSpiH1XzNZIu6MTI2RaSaZXMmobM3YJo21jjPWeXTdOWUkVyF1esSsClO5tu0sAleF330FCNUgZUgCEsURcPZgSCCqgZV43hh8dU40e3Ho7vD8oaZhKBpGpqb6lDpceCFxTOgaRyCwOCWwtVQ19wYbmWvf8DWjHJh25IZUDngdggY6znf7E3TOPwhBW+0daCzN2hUg3VKDM99LbyOXNU4RssSpLiFbskkD122ePm+WRgMalAijbkkkWHbkhlQNA6BMZztD2DtV/4KDlFAjz+ER3cfwmO3XJHVVf9WUpIdOaUUXTJ26fGruGCU03i/JIHBJTH0+NWMG6sRww9VYCUIwhRF0fDx2X509gZiHAs/uu1KPPTlBnz/lbaE6qiaxnGm/7zcoS8Sffbtj3DnrIvx7Nsf4Vt/MxmTa8oBmMsdYz3n5ZlDp3tx6twgaitkHGjvsawGu33pzIT5W0keqsahRX5O9gRii64tmIZ/++XhmKJrXreE77/ShgPtPaitkKFxZM2Zkql7phRdMnYZ6xFxtCux5fwllaUjRY0kHCaOttoKOSsVWClXRhBFTEdfAO1n/Qmp02+++Ad094dMm7p19QexdEusA2XlzoNG07nmpjpDRrDbTC7aNWMm0bSYSDRAWPLYvCg2jb+uuREPv9aGrv4gOvoCCW6Ze5/fH+P4WbHjILr7Q1g2Z5LRaM8lsaw5UzKVWUrRJWOXHr9mBCJA5P3b2ooePy1gLUaqvS60xMluVr/b6UKZEYIoYkKqhjKnaO6KKXOgqtwFBhhrMOJdLzH7Rxww+r+6jJBMYtDHinfNTKwsw/YlMxDSOByigGqvK0GiAcILNsd6nDEOGd0989ANKlQttePneLcfY71OVHiceP7vr4ZTFFDlDctI2XCmZCqzlKJLxi6KxftHRc+KE0kSMKWmHNuXzoSiapCS/G6nPXYW5kcQOYXK8FvjEAUMBFXT1Olo2YHbogqa6dKClWygO2D0f3UZIZnEED1WtGtm1/LZGDfa3rclQRBMZR3ZKaI/YH5t0Y6faxuqwQHTa82GMyUbMkupuWTsQm6a0kOSBFzok7M+Lsk0BFHEVHtdqBsjJzpXFkzD2l+8Z9ulsq65ETtb241/Ny9qQqXHmVJiyIYEYTWGonGcOjeIx2+5IuHaoh0/q750GZY/vz9nbpWRLLNkitshJBSq27hgGtwO+ughYinqRnnZhBrljUxKoVFetJtG03hkMRnHrLW/wtQ6H5bNmWRIII21o6FpHLJThKJxDIZUAAwC49A4w0AghGNn/biydjRqRoc/QNJpJudxiRgIalBULex8EZjhykkmS5id4+S5sPyz9hfv4zvXXopxo90QGUNQVeF1ORBSw+4axjg+u25vwphvrfxC1pqx5aqAWpbI+0Ss7s9jXf343ZEzmFVfBTXihnr7cCeunjQWEyszrJJFFAsjolEeQYx4JElA9Sh3lOvjd1g9rwHXNlTjzlkXY+XO8y6bjQum4aGX/4TOvgCevGM6HCLDXU+fL2CkZ0amTagwxrfbTE5RNLx/ujfG+aK7dHR3TjrN5JySiIGgis6+ABY+9XsA5/vp3PPs+XO0LGzCtQ3VMU30su1WGakyS6Z4nCKmXDg6RkLbuGAaPM7SdxIR6UG5MoIoEaJdHy17j2DVly4zAhEgLF8sf34/ls2ZZEgZ7Wf9Ca6aB69vGJIEYeZ8iXfnpEOlx4mJlWUxEpRVP51VX7osRgrQZSYivwQULUFCW/78fgQsujYTIxfKjBBEiRDt+jjQ3oNz/pCpk2FSlQfblsxAjz+EsV5nwvNipGy8FVaShVUfEp/sQJXXhaCi4kT3ABySAElg8AeTSx6CwHBRpQe+Mge2LZkBjQOaRT+dc/5QjCNnbGHJKCMWctMQdqFghCBKhHjXR0dvwNTJ0H7Wj7ufecdImU+t8xmN6FLJG8kKgFkVRNI4xwPXTcatUan69fMb8ejuQ4ZcZCXhCALDGI8LmhxbXC3+HB29ASzd0mo83rV8dmYvJpEVyE1D2IVkGoIoEeILiO1sbU9wMqyf34gNew4DOJ8yv39uvfF8KpdIsgJgZgWR1jU3gjFm2s8iWi5KJeGYFVfTz9Fi0k+HJJrCgNw0hF0oM0IQJYIgMNSUu2Lae+/+35NYPa8Bl40rhygw3PfCASMLAkRkm2ov3lr5BVsukWQFwCTJhcnV3rg+JAIGQtZF1qKPT4amaYYMo3Fu9KKprZBRU+7GIzc14qEbCtLpMqLpC6jY+ptjCS3nv37Np1DpzffsiEKCghGCKBE0jeN0RK6Id7OsbW5E36CCzr5AzDG1FTJkh2jbKZKsAJimcXx4pj9Bwqke5TQ9Rm+uZUcaMuul89T/HMUjNzVCkgRyuhQoDlHA20e7sL31uLGttkLGP/zNpXmcFVGIUK6MIEoEq54zD17fAEXjePi1tgSJI13XSbICYFYSTjDEE4qyrZ/fCDGynsCONGR1XSTHFDYSg+l7L1HiioiDMiMEUQJoGoc/pJjKIaLAEFI0vNHWgc7eYEauk2R9VqwknJCq4dHdh2LO++juQ9i4YCq2L50JzjnO9AcsHTZW44qR5zt7A4VajGzE41c07Np/wlSmIYhoKBghiCJHd7hYOU2ie8zo/WP0x0NxnVgVALOScCRRQGffebcLEO4nc3YgFCMpWTlsrMaVnaKls4cCksJAdoi4adp43P3MOzHvs+ygomdELEUt0zDG6hhjv2KMtTHG/sQY+2Zk+xjG2JuMscORfytSjUUQxUoyp4kugQxHfxWrc1R7XQnbH7y+IUF6sXLYJOtdY+XsIQoDRdVMnVSKSkXPiFiKPTOiAPgO53w/Y6wcQCtj7E0AdwHYwzlfyxhbBWAVgJV5nCdB5Axdxjje7ccPXj8vh+hOE71AWc0oF15aPgshRUvZYyaV5GG1r5WEE7/dSnq5cLQbmxc1wSc7EFRUaBo3jn/1G7PRH1ChaBwOUYCqmRdZS+XMIYaPkMYx65JKLP7cJTEyTYiKnhFxFHUwwjk/CeBk5P+9jLH3AIwHcCOAOZHdngWwFxSMECVKtIyhyzC1FTJeuW82Dnf22ZIxkhUzS3dfMwknfnunSUG2axuqoXHEuGb0cTWN43j3YEzfm+HoSUNkhtclYuHMiTEyzcYF0+B10XtExFLUMk00jLGLAEwF8DsANZFABQBOAajJ07QIIudkQ8ZIVswsk33TmfOqL12Gr7+w33Rcs743y7a24p/+tiGn0hORGYMh8940gyGSaYhYijozosMY8wLYCeAfOOefMHb+mxznnDPGTHOCjLElAJYAwIQJE4ZjqgRhG7v3Z7wMwhiDU2QYVDQ8dvMV6PGH8MHJT3DdX10AMeJ6URQNknT+u0iyYmbxpLOvnTlrmgaVAyE1XNisZe8RozDb8W4//CEV3KInDWOIKYB2wWiZFq8OE3buT+pNQ9il6DMjjDEHwoHI85zzlyKbTzPGLog8fwGADrNjOedPcM6nc86nV1VVDc+ECcIm6dyfgsBQ6XHik0EF33vlXRw63Yfbnvgtbn3it9j/cRfmXFaDu595B9c89t+49Ynf4v3TvVCiOqfqUk80VpJHOvvamfPZgRBu2fwbfH79Xqx5tQ3f/eJkTK3zGeMe6egzapLEn/NoZz8YY3jqf47CKYkUiAwjdu5PPUiMprZChkMs+o8eIssU9R3BwimQpwC8xzn//6KeegXAnZH/3wng5eGeG0EMN7p80txUh5U7zzsY5k+fgHtNJI6OqGqs6bhtsunMMZN8Vu4Mu2r0Sqsb9hzGlrc/wiaTvjcb9hymAmgFjGhR9EykmJGIo9hlmtkAFgH4X8bYHyLb/gnAWgDbGWP3ADgG4JY8zY8ghg1dPvHJjpjUuCgw81R5lL0ymRMGSHTP1Fd5jX0dkgBJYDh5zp9W4bFkhdrqq1i15CkAACAASURBVL1YPa8BP3j9EA6094QX5s6ZhBeXzMCJSCE1gQGrvjQFPf4QXJJAWZECZFAxL3j3w9uuzPfUiAKjqIMRzvn/ALD6CzR3OOdCEPlGl096/KEYp4qqcctiZNFYOWGSuWcADKnwWKpCbce6BhKKpJ08F0DHJwH87PfHcOesi436FXpZ+6pyNwUkBYYksISCd7UVMiR6n4g4ilqmIQjiPLp8srO1Pab42Y59f06QOFoWNqHaa6+5XDL3zFCdNakKtU2sLDMtkrZhz2Gs+tJlMTLU8W4/lm5ppWJnBYhLErBxwbSY93LjgmlwSfTRQ8RS1JkRgiDOo0stj9zUCE3TjL4vTkmEzy1h+9KZUFQNkiig2uuKcdMkI5V7ZijOmmSF2i4YHf7gMiuSdrzbj3P+EBU7KxL6gyq2/uaYaW+asfmeHFFQUDBCECWEldQCABf6ZNPtqbDqDRPd88bqOTtjRhdq27V8tiG1WBVJ6zApmEbFzgoTSWB4+2gXtrceN7bVVsj45l/X53FWRCFCuTKCIJKSzD0zVGdNusdF79+y90iCQ4OKnRUmY8ucCRLhpoVNGFtG7xURC+Ocis8AwPTp0/m+ffuS7nPRqteGaTbEcPHx2uvt7Jb31XZ27s9ckqxvTTo9beyOmWp/2SlC0bhln50RRt4vPNn9GQgoODMQhKJxSALD2DInXC5Kyo8gbN2fdEcQBJGSZPJPsueGOmY2z0PkF5dLwngKPogUkExDEARBEEReoWCEIAiCIIi8QsEIQRAEQRB5hYIRgiAIgiDyCgUjBEEQBEHkFbL2RmCMdSLcVG8ojAVwJovTKSRK+doAe9d3hnN+3XBMxooM789cU0z3SDHNFSit+7PYXvuhQtcZi637k4KRLMAY28c5n57veeSCUr42oPSvbzgoptewmOYKFN98k1FK15IMus6hQTINQRAEQRB5hYIRgiAIgiDyCgUj2eGJfE8gh5TytQGlf33DQTG9hsU0V6D45puMUrqWZNB1DgFaM0IQBEEQRF6hzAhBEARBEHmFghGCIAiCIPIKBSMEQRAEQeQVCkYIgiAIgsgrFIwQBEEQBJFXKBghCIIgCCKvUDBCEARBEEReoWCEIAiCIIi8QsEIQRAEQRB5hYIRgiAIgiDyCgUjBEEQBEHkFQpGCIIgCILIKxSMEARBEASRVygYIQiCIAgir1AwEuG6667jAOiHfsx+8g7dn/ST5Cfv0P1JP0l+bEHBSIQzZ87kewoEYQndn0QhQ/cnkSkUjBAEQRAEkVcoGCEIgiAIIq9QMEIQBEEQRF6hYIQgCIIgiLySs2CEMfZTxlgHY+zdqG3fY4ydYIz9IfLzt1HP/SNj7EPG2CHG2Bejtl8X2fYhY2xV1PaLGWO/i2zfxhhzRra7Io8/jDx/Ua6ukSAIgiCIzJFyOPYzAH4M4Lm47Y9zzn8QvYEx1gDgNgCfBnAhgP9ijF0aefonAP4GwHEA7zDGXuGctwFYFxnrRcZYC4B7AGyK/NvNOf8UY+y2yH635uICCwFN4+jqDyKoqHBKIio9TggCy/e0skapXx8R5qJVr9ne9+O11+dwJgRBJENRNHT0BRBSNThEAdVeFyQp87xGzoIRzvmv08hK3AjgRc55AMBHjLEPAVwVee5DzvlRAGCMvQjgRsbYewCuAXB7ZJ9nAXwP4WDkxsj/AWAHgB8zxhjn3LbfuVjQNI5Dp3ux+Ll9ON7tx7UN1Xjw+gaIAsvZB/dwBgfx11dbIePJO6Zjck05BSQEQRDDjKJo+PhsP9rP+lHmFDEQVDEwRsFFYzwZByS5zIxYcR9j7A4A+wB8h3PeDWA8gN9G7XM8sg0A2uO2Xw2gEkAP51wx2X+8fgznXGGMnYvsX5RG+GQf/l39QeODemqdD3fOuhi3/5/f5eyDe7iDg+jrA4Dj3X4sfm4fdi2fjapyV9bPRxAEQVhzdiCIzt4AVr/8rvEZsH5+I0a5Hage5c5o7OFewLoJwCQAVwI4CeCxYT5/DIyxJYyxfYyxfZ2dnfmciin6h/9NG9/C7HW/wk0b38Kh073QtHCSJ6ioxgf1sjmTsHLnwYQP7h5/+OY50T2Azt6AcexQsAoOuvqDGV6pOdHXp3O824+goubkfIVGod+fxMiG7s+RR1DVsGJH7OfMih0HEVS1jMce1mCEc36ac65yzjUAT+K8FHMCQF3UrrWRbVbbuwD4GGNS3PaYsSLPj47sbzafJzjn0znn06uqqjK9vKyT6sPfKYmorZABAD7ZkfDBXeV14WTPoGkwo2k87SBluIIDfW4q53j6rs9gap3PeK62QoZTErN6vkKl0O9PYmRD9+fIQ9M4Zl1SiTe/9Tn88jufx5vf+hxmXVKZ0ZdcnWENRhhjF0Q9vAmA7rR5BcBtESfMxQDqAfwewDsA6iPOGSfCi1xfiaz/+BWA+ZHj7wTwctRYd0b+Px/AL4t1vUiqD/9KjxNP3jEdtRUyevwhIzDRuX9uPZZubTXNliTLuFgRHfzoZDs4iM4Gfe7RvVj98rt44LrJmFrnM2ShSo8za+cjCIIg7FHmFLFw5kTc/cw7uOax/8bdz7yDhTMnosyZ+WdAztaMMMZ+BmAOgLGMseMAHgIwhzF2JcLNcz4GsBQAOOd/YoxtB9AGQAHwdc65GhnnPgCvAxAB/JRz/qfIKVYCeJEx9jCAAwCeimx/CsCWyCLYswgHMEWJ/uEfHZBEf/gLAsPkmnLsWj4bmqZh86ImLN3Samh5F4/1xBw7tc6HZXMmoXdQwalzg6jyunC82297LYYe/MSvGbETHNhd+GqWDVqx4yC2LZkxpAWz5MYhCILIDgFFw/6Pu/DC4hnQOIfAGH7ZdhKVn74g9cEpyKWb5qsmm58y2abv/wiAR0y2/yeA/zTZfhTnZZ7o7YMAbk5rsgWKnQ9/QWBGAFFV7sau5bOND14ObgQzU+t8+O4XJxvrSmorZKxrbsQPXj+EA+09tuSW6OAnnQ/3dBa+WmWDdE6e82d03s2LmjDW44QgCBSYEARBpIHbIaDp4rG4/cnfGn9TNy1sgtuRuchCFVgLmOgP/7dWfgG7ls9O6lzRA5PxFWWoKndhrMdlyDhmC1xX7jyIZXMmAQhnXBg7P67VmpL4c9j5ME9n4auVFKRqPG1Zyey8S7e04g/Hz9kegyAIgggzGNJwb5z0f+/WVgyGimwBK5E+Q/nwjz5WD2amjCs3zTj4ZIeRJREjQ6dy8aRLfLZjap0Pq+c1IKSq+EuPPybgiV4HA8DIZjz8WlvaLh6rLIu+2DeXTiCCIMIMZbE8UZgoGjf9m6pk4T3NR50RYhjRg5nOXpiuP6kud2H1vAY8+/ZHeOSmRgDp1/dItS4jeu2LLhc9+/ZH8LoujpGNdOkmXgrSNA1vtHXEnNOOrGS15qbHH7I9BkEQQ4cKF5YWDoHh2oZqNDfVwSc70OMPYWdrOxxZeC8pMzJCMMs4rJ/fiG9v/yPWvNqGb/3NZGMtSjoWXjtZlOhzL5szCc++/RFWfHGKaV2Urv5gTDao0uOEyoEdy2Zi86Imw+Zrx8Vjds3rmhvRsveI7TEIghg6w12biMgtLoeAb1xTjzWvtuHWJ36LNa+24RvX1MOVhTUjlBkpEHLt+ohffOp2CgiGOH5425VGfwH9fKlcPNHYyaJEnzukqvC6LsY5fyhlwGP2rWpdcyOeffujmODJ7jWrGsfDr7XhQHsP2YQJYhgY6YULS43BkIZ7n98fu2bk+f3YtmRGxmNTMFIADFcqU884pDpfOhZeu39s9HP/pSe8cHb1vIaUAY9ZoLNy50FsXzoT40a5bb020W4jTeN45KZGPHQD2XwJYjhI54sNUfhYrRlRi63oGWGO3VSm2UKwoSwOS3W+dFw86RZC4zx8M7fsPYJ1zY0xEkp8wGMV6HDOhxREZLIYmCCI9DGTSikjWbyIAjP9e5+Nv6WUGSkA7GQXzLIZz33tKgQULe2MSrLzxbeHril3J+3GmG4hND14OdDegx+8fgir5zWg0uPEhT7ZyHbokhVgvuiWvlURRHEgCAz1VV5sXzozpuU8fREoTiSBYf38RqM/jb72UKJgpDSwk8o0y2Yc6xowuifq2+xUUrU6n0MU8P7pXizber6Ka8vCJkypKTcNSPSgYUyZA9uXzgTnPKX8USE70LKwCcu2tuJAew/WvNqGloVNxh+o6KCryutKuPGTBTpUbZUgCgtN4zjc2UdumhJBEBjKnCLW3Hg5ypwiBoIqypxiVt5LkmkKADupTLNsRplTHNLiMKvzATACEX2sZVtb0dEXSBgj2kVz9f/7S9yy+Tf4ZFBJGQB0+0PYsOcDrJ7XgG1LZmD1vAZs2PMBuiN22+ig60B7Dx7dfQhrbrwcv34guVyU7dooBEFkzpn+gKkkfKY/8W8KUfhwi7+nVtvTgYKRAsDOGg2ztRkDQXVIjeuszucPmcs3ikl7aKt1J2f6A0nXsAQVFZ29sWthOnuDRgAVH3QdaO/B3c+8A5Eh6ToPshASROExaPE3JRsVO4nhZ1DR8Pxv/4zaChlV5S7UVsh4/rd/xqCS+ftJMk2BEO36MMNsbcbEyrIhN64zO59DFEzlG0lMjFmt1p0MBFQsfOp3lilZ2SnigesmJ2iOcqTrY7qr73VpZiCo2Fp3QzIOQQwfImOmv88i/doVJbIkYMGMCTje7TdkmgUzJkBOsq7QLhSMFAlWTeoApN24zopqr8tYzxG9ZqTamxgkOSXRtBLfR2f6k65hUTRuBCL6Pit2HMRLy2cBSG9BbPT6klRWYaoESRDDj+wUTRc8ylloOU/kAcYQVDRjrWJthYzHb7kCYLSAdURhlT1JllFJB0kSMKWmHNuXzoSiapAiK9/NFq9WyA7cP/fSmMBl08ImbHn745j94rMTIUUzzWCEImm+dDoDR0szulU4vry8HsSkW+KeIIjM8clO1Ixyxyx4rBnlhk8ma28xElI1fGv7H2P+jn5r+x+p6BmRfSRJwIU+OeV+3f5QwmLXe7e2Ys2Nl2N763Fjv3iJxY4Mk0qy0omWiqKtwpeNK4fslGKCGKoESRDDjyAwXFTpQbnbQfJoCVCURc8YYz9ljHUwxt6N2raeMfY+Y+wgY2wXY8wX2X4R+//Ze/c4Kcor///9VN/nAsNlwAsQ0CBmQkZhEBC/yRr9anBFCYFolIuikVtcs65RzDdhdYPuT0TX1RhuJoqIRgjoaryghoS4qyHqSELciaiIBgjCAAPMpadv9fz+6Kqiuruqp3u6Z4YZn/frNS+G6ro8VVNdz6lzPuccIcJCiD8ZPyts29QIIf4ihPhICPGQMPrcCyH6CiFeE0J8aPzbx1gujPU+Mo4zuqPOsbtRzO6ZbpP7sP6lWbOCilkEKV3Ua6YKh/zeDLFrvsXZFApFcVDFBnsO3bXo2WrgYWCNbdlrwA+llHEhxBLgh8BC47OdUsqzHfazHLgB+CPwEjAReBm4HdgspbxHCHG78f+FwCXAcONnnLH9uOKeWvdD1yWfHGrm00Mtlrv0C/1KGNqvtF03kpuHoyTgyRpiyScM0xb9Sv2suW5sxjk5GTb5FmdTKBQKRSohn+asATqRG+VJKV8XQgxNW/aq7b9bgWnZ9iGEOBnoJaXcavx/DfBNksbIZOB8Y9XHgS0kjZHJwBoppQS2CiEqhBAnSyn3FXhK3Zoj4Sj7j7WmCI+WTqumosRH39L8NRNuk3v/0rbffHINw+RCJE1MZdZLcTpmsYwghUKh+Dzi9Qj6lwdSNED9ywN4i5Ae1ZV1Rq4jaVSYDBNCbBNC/F4I8VVj2anAHts6e4xlAANtBsZnwEDbNrtdtukWFDOcYhKOJhyzWMLR9mkm8ulf01HkW1tEuYsVCoWi/TS1Jli66X2iRu2paEJn6ab3aWotXHvXJQJWIcSPgDjwpLFoHzBESnlICFED/JcQ4su57k9KKYUQec/YQog5wByAIUOG5Lt5h9BRKagJ6SI8Srtq+dTiKKaHoz1kE6X2hJoiJ+L9qVCYqPvz80dcl45FK+OdJWAVQlwmhCiKF0UIcS0wCZhuhFKQUkaklIeM32uBncAZwF5gkG3zQcYygP1GGMcM5xwwlu8FBrtsk4KUcpWUcoyUckxlZWURzq5wOqqSaNDnLOAM2mJ93a2kupso1efVutV5uHEi3p8KhYm6Pz9/BL0at00cweIX6rhy1VYWv1DHbRNHECxC0bNc93Al8KEQ4l4hxJntPZgQYiJwG3C5lLLFtrxSCOExfj+NpPj0YyMMc0wIMd7IopkFPGds9jxwjfH7NWnLZxlZNeOBo91JL5JvCmquIZ3+pQHHLJb+Nr1IZ5VUL1YYyi0zx6sJVRpeoVAoikxC4hjuT/ewt4ecwjRSyhlCiF7AVcBqIyTyGPBLKWWj0zZCiF+SFJj2F0LsAe4gmT0TAF4zMnS3SinnAV8DfiKEiAE6ME9KedjY1QKSmTkhkhoTU2dyD7BeCHE98ClwhbH8JeAfgY+AFmB2LufYFTiFEnKpw2HfLqFL7nqxjlfrDmQN6eTSyrszanEUMwzlJkrddzSsaoooFCcIPSFkqkgSTzgXrXTqX5YvOWtGpJTHhBAbSBoF/wxMAW4VQjwkpfypw/pXOezmFy773ghsdPnsHWCkw/JDwIUOyyXwvSynckLgNikPryzLmoKavt3FVQO4/ZIvMf/8L3KgMcIDr+3g7inVGVqOXFp559sXJpdzTH8IFbsSqpNupdjnoVAo2odqw9CzMOuMZPQaKsLfMlfNyGQhxLMk02d9wFgp5SXAWcAtBY/ic4jbpNwQjrlmqei65LNjrTRH4iyaVMUVNYO4ZsIwZj36FlOWvcniF+q4ZsIwdD33Lrv20EUxC5K56U86w/tSzPNQKBTt52BzxLW7t6L7oQlYMrU65dm6ZGo1xbArc/WMTAEekFK+bl8opWwxwiSKPMk2KTu97Tu9Yay5biyzHn0r5Yu+cON21s0Zn+GVyMUIKGYtDjfjZ/3cczvca6FqiigUJwaRmPNzJxIr3K2v6HwSEh5/cxeLJlVZDVIff3MX/3pZzsmvrrRpjBjC0i+kGyImUsrNBY/ic0i+oQSnyf1wc9QlXTfTcHnqu+NyOl6x0nXdjB+PIK9KqO2NN3d12rFCoQCPEI7dvYtQI0vRBXg1wezzhmVUYPV2Rjl4KWVCCKELIXpLKY8WfEQFkH95cqfJ/VBz1Dl+JzKzSe56sY6VM2uY+0RtxvE6QmCWbmyNGlzBTRcOJ5LQGdgrwDMLJhCL61mPp+LNCkX3xufVuPGC4Sx48l3rO7xs+mh8RUgFVXQ+mhBUlvtZPXssmoBkIqSOJjqvN00T8BchxGtAs7lQSnlTwSP4nJJvKMHJk7KxdjcrZ9Qwd21tipXq5DF5te4AiyePzDge0O4JP5sRYze2KssC3DZxRIo1ncsxii12VSgUnUskrvPwbz9Mces//NsPi+LWV3Q+FUEvBxojzFv7lvUsXzGjhiEVhddPzXUPzxg/iiKSTyjByZNy80Uj+GL/UtbPPZd4QmdnfTP3btrBLRef4egxEQ7HO9DY6jjhP7NgAgPKg67jactrkW5sXblqa95GRWeIXRUKRcfhEXDNhGEs3Hj8RWTJ1GoVpummHGyJMc94+YXk83je2lrWzz2XU/yFGSS51hl5vKCjKAommyfllIoQextamL36bSCZfuXUWdEprtfqIjBrbUNglovXwjS29ja0tMuoUCm6CkX3RpdYhgikiuwV3Y+YS52RWBHqjOSa2jtcCLFBCFEnhPjY/Cn46Iq8yNbozV4aXROCezftYNGkKtbNGc+iSVXcu2mHY1M8jxCOJdXbenPJx2vhVra9LaNCpegqFN0b3aUnVjfrzKAw8GrO80UxBKy5qogeA5aTbG73dWANsLbgoyuKhn3iPhKOUd8UYe4TtVy5aitzn6ilvimCECKj9HrI72HptNS88aXTqgn5nQ0Fs5S7ua4dNwOjvUaFW2dgoOBy8h3RGVmhUKQScOmJFfApAWt3JOjTWD59dMqzfPn00Sk9ztpLrkGekJRysxBCSCk/Be4UQtQC/1rwCBQ5k00wap+4dV3PyJxZMrWaO59/j5svGpEiHK0I+RnYK8jiySMp8XtoiSYY2CtIr4CP+saIq9i1siyQEQpyMzByKUXvRrquphgZNipLR6HoHPqG/KyYUWPpDEzBY9+Q8m52R8p8XkJ+T8p8EfJ7KPN1noA1YnTt/VAIcSPJLrhlBR9dkTO5TKD2ibuyPMj6uefy9yNhDjVHue+VHWzbfYS6fY0Zuo6h/UopD/qIxpM3Vjwh2XMkzK6DzTy0+UPqmyJJQ6PMbx1/T0OYezftYPHkkZw+oIyQL3uKblul6HOlGBk2KktHoegcGsIxHtr8QUo2zUObP3BsWaE48TkUjnHtY29n6PjWzz2XUwKdIGAFvg+UADcBi4ELON4xV9EJ5DuBappASsm0FX9IWe6k6zCNGCeDZ8nUau57ZQc3rHmHp24Yl3ITbtt9hNmr3+aNhV/P+mA51Bzlgdd2pDyQ3HrotEUxMmxUlo5C0TlE4wlerTvAq3UHUpbfcZn6rnVH3ASsndYoT0r5tvFrEydwF9yeTHsm0GJUeV24cTuLJlUx94la12qKbQlRdV13TO9z6qHjvg9p9dFxO6dci7epLJ38GXr7i3mt/8k9l3bQSBTdCfVd61l4NZeKuh1dgVUI8WvAVdknpby84BEocqI9X+piVHnd0xCmIuRjUJ8QpQEPN114Rkb8t0/Il3XsCZf0vvVzz83p3O0eGyetyooZNVQEvTnrQPK9LgqFon2o71rPIuhSUTdYhIq6bXlG7iv4CIqi0J4vdTGqvA7qE6IlmuCRWWOIJqRjwZu2tBbSJb1PytwyWOweG7tWZXDfEDvrm3lo8wfcefnInMNYhQhqFQpF7qimlT2LcFy3DBFIPmcXPPkuTxehbkxWY0RK+ftCdi6EeBSYBByQUo40lvUF1gFDgU+AK6SUDUIIATwI/CPQAlwrpXzX2OYa4MfGbu8yi7AJIWqA1UAIeAn4vpRSuh2jkHPpaty+1EBG1ov9i15oldeVM2o4uSJIRcjPvqPhLilelu6xMbUq6+aMZ+4TtQD8+FLnWGY0nnDMCiqWoFahUGRHNa3sOSR05xfLRBFKI3R00bPVwMS0ZbcDm6WUw4HNxv8BLgGGGz9zSNY1MY2XO4BxwFjgDiFEH2Ob5cANtu0mtnGMbk160TNIptpOWfYG5y35HVOWvcGO/Y2uNTPaqq3hVNfjSyf3om9p0mvQVcXL3I57JByzfvd6NMd1ErrMuD4HmyOOXhRTk6JQKBSKTHwuRc98J3rRMynl68DhtMWTAbO8/OPAN23L18gkW4EKIcTJwDeA16SUhw3vxmvAROOzXlLKrTLp71+Tti+nY/Qo3DJsnCZVU3fRluGSrcprsYuX5eqFcDru0mnVrNiy0xrDgLJAxjorZ9Zw14t1GdfHrQS+yqZRKBQKd0oDGstn1KQWPZtRQ2mgexY9Gyil3Gf8/hkw0Pj9VGC3bb09xrJsy/c4LM92jBSEEHNIemEYMmRIO06la8klw8aeYVJobY1C4r+FuGrTj+vzang1wcNXj0oZQ/rYdF3PSCnc0xC2SuCf6Ar/7n5/Kno26v78/NEU0flpWt2Yn27+gDsu+zK9Swrbd5cWPTP0HR1ahzvbMaSUq4BVAGPGjOnSeuC5pqXaaUuLYc9Cuf/bZ+XkDWhrHPkYFW77as+5Oh63NPs69Y0Rx+sT8nu6hcL/RLo/FYp0cr0/2/N9V5yYJKR0rBuzaFJVwfvuiqJn+4UQJ0sp9xmhFvOs9gKDbesNMpbtBc5PW77FWD7IYf1sxzghaW958rYybOxhnCPhWJvegGKWSXfb1/DKsk4Tj/Yr9bPmurF8eqjFKl38hX4lVIT8VIT8SuGvUHQwqvVCz8KraY7ziEcrPEyT0x6klG9LKZuklHuAfwGmGrqO9vA8xw2Za4DnbMtniSTjgaNGqOUV4GIhRB9DuHox8Irx2TEhxHgjE2dW2r6cjnFCko/2w05bWgx7GGfFlp0smVqdVe/R3nHkc04HmjpXPBqJ6yx67j2uXLWVRc+9RySeLLSWTRujUCiKQzGfKYquxyNwbKzaVpf3XGir6Nm/AuullO8LIQLAJuAsIC6EuFpK+Zs2tv8lSa9GfyHEHpJZMfcA64UQ1wOfAlcYq79EMq33I5KpvbMBpJSHhRCLAbMK7E+klKYodgHHU3tfNn7IcowTkkLKk2cLm9jDONt2H+G+V473kgn6krqLfUfDlmegmGXS3fYVdykn3BHiUdWDRqHoWlTrhZ5Fa1zn3k2prT3u3bSDB79zdsH7bitMcyXJsAwc9zRUAmeQzFLJaoxIKa9y+ehCh3Ul8D2X/TwKPOqw/B1gpMPyQ07HOFHpqJLJ6WGc+qYIJ/UOckqvoGOopF+Zv2jjcDsnMwW3M8Sj6kGoUHQtqhx8z8KrCeqbIlZ9JzDDNB2f2huVx8tkfgN4WkqZkFL+ldz1Joo2KLQOhxv2SqOv33o+6+eey/DKMhrCMUePgVcTRRuH2zk5peB2lHi0vXVRFApFceioZ5uia/B5NMcwjc/T8am9ESHESGA/yfoiP7B9VmAiz+cXJ3W5aTTEEzreIpUn13Xp6AHpFfQ6egzC0USbqbu5KuOzpQHnU4q9ECW+6ovRdeTbWE/RM9E0wRf7l7JuznjiusSrCdV6oRsTTeg8++5eHrv2HDyaIKFLHnn9Y77/f4cXvO+2jJF/BjaQDM08IKXcBSCE+EdgW8FH/xxhTqq6rnOwOcrcJ2pTJsiygIePDjRT4vegieQfWRO4psQKIfAI0DTNdYJ200ysn3uuq+s0mwYlX2W8077sBlJlWYCbLhxOtL9OScBD/9JAhuFTiBJf9cVQKLqWeFzn04YWdh8OWxlt4ViCoX1L8Rah+/MNagAAIABJREFUuZqic/F7Nb49ZhCzV79tPZMfuOIsfB3dKM/ImDnTYflLJAWnCoNsb/D2SXXRpCoWv5BZFfSJ68ey6Ln3qCwLcNvEEVz1yNY2U2KXTK3m8Td3cfNFIxwnaDfNhEfQLo9BvoJQp2ti7qOyLMDtl5zJLb/68/E+ODNr6F/qtwysYghQ7QZRT693kK834pN7Lu2gkSgUSRrCURqaoyx67r2Uyat3yEdlebCrh6fIk3hC8sh/f5wiYH3kvz/mzsszpJt501Y2zb9k+1xK+R8Fj6AH0NYbvH1SrQj5HA2EQ01R9jSEWTSpils3bHf0ZqRPzAs3bmfRpCrXCdrndRaLijw9BuYk3hKNs2hSFSu27GTb7iPWOJwEoW7XpG9J8vzv+dZXLEPE3M/cJ2q551tf4fZn/pI1nNQeAaqqd6BQdD7RuM7N61O/5zev/zPritDlVdEVSBZ8/Ys0NCf7gvk9Ggu+/kUEHd8or9z4GQPM53gZ9nnA6IKP3k1wazBnLt93NJw1l97uoTCLj9kZ1CdE75CPUYMrXI2VmEtK7CkVIRZNqqIlGs9ofufVhKPYyKuJnOts2Hva/MPSLSx+oY4ffGMEowZXWPt0EoS6eTUSMrnNSb2DjudjLr9hzTsI4dyUqT0CVFXvQKHofOId2OVV0fl4hCAcTaTUbgpHE2iig7NppJT/JqX8N5LVTUdLKW+RUt4C1ACfi2YETg3m/vrZMfYfDbOnoYUfPZv0YmR7g7dndTgVH1sytZqlr7zPD74xglhCd5yAvS7dEitCPha/UMc/LN2S0fwuHE1YOeHr5oxn0aQq7t20g3A0d8+C0yS+cON25p1/etbwjluISErJI7PG4HE5H49xU9vDScVQ4qs0X4Wi83H7nitvZPckpssMz/2tG7YTK4JxmWt67kDA/goZxaX5XE/DaTKe+0Stpf1YMrXaMiDccunTy5JLYN2c8RwNx/B5NFpjCabWDObxN3cx+7xhLJ1Wbf3BB/UJsWz6aHwewZKp1SzceHz5kqnVHGuNuWoq/F6PY054Pp4Ft0n8Syclwzxu4Z1s9QVGDAxR39iacZ5Lp1Xz2bFWa11N04omQFX1DhSKzsenCR644iwrVGMJHpUx0i1JuHi60ru/t4dcjZE1wFtCiGeN/3+TZNGzHo/bZGyGUxZu3M7SadUZhkL6G7xZltz8fMWMGuK6zhxbVo3pMfnsaIS114+joSVKcyROJKYTTUgef3NXinDo8Td3MbVmcMbYzLf9YqS2uk3iIb83q4g027FNYyLk97B48khLZV/i93Dn83UZ6xajWmr6eC6uGsCPL60iGk9Q3xjpcWJWheJEQAjoXeJL+Z73LvFRBK++ogvwu+gQOzybxkRKebcQ4mXgq8ai2VLKz0Vqr9tkfCQcY9TgCuadfzonV4TQdcmy6aOpKPET8nmsCb++MUI0nsjwrsxbW8viySMzwh/r5ozncEuUf3/prwD84BsjuHn9n6wsG7snYeXMGh78zQcp47W/7RcjtbW9Bo29nohT7RRN01j2u4+YWjOYEjz4PIJoXPLgVaOs69ee+ibZCHg1Fk8eSf8yPxK4+ud/VGJWhaIDiSUk972yw/qeRxM6972ygzsu+3JXD03RDkI+jeUzapi/9vhL9PIZNYR8nWSMGJQAx6SUjwkhKoUQw8y6Iz2ZPiEfK2bUMG9tqgfjuW17+cE3RqR4Q5bPqOGkMj9HIwn2HU2KtO56sY7r/89pjt6V/mV+Vs6ssTwdK7bsJK5LK/V35cwaa/97GsLcuynZW+a0ylJ8Ho3KUj83XzSCun2NroaCm2chHtc50BSxCo+V+DWaI5kTfbpR4fNoeDTB7oYWq2CZU70At4Jr5oTfzxh7+ueDKjLjycXIhDnUHGXWo29Z19UpvVr1rFEoioumwc0XncFnRyNAMvvi5ovOoAhNXhVdQDQu+enmD1I89D/d/AF3ffMrBe87J2NECHEHyYyaEcBjgA9YC5xX8AhOcBrCMR4yLv6A8gC9Qz7uefmvTK0ZbBkKkJzQ5q+t5ek54/nOqq0phouTpuTiqgFIsCZFUzPh9xyPsTpl1kQTOgld8nF9I639ShheWZZ3xVRdl7y/vzHFwFo+fTRP/OFTjoSj/PjSKjyawO/10Cfk428NLXx6qIWKEh/9y/x8ergVAbREE7T0jacUMDKPF47F+exoK5VlAcuYsk/4+XhtilFvxB5uc8tYUmJWhaK4eIRGLCFTQtTLpo/GI5Q10h1pjSd4te4Ar9YdSFn+40mFPztz9YxMAUYB7wJIKf8uhCgv+OjdgGjaxTdDM2eeVO4yoekpk6abpuRHl1Yx3QgTmOveuiEZpjFjrAPKA5YRM2pwRYYnZum0aipKfHlXTK0o8VmGiHns+U++y9rrx7H3SDglfLFyZg3xhJ5SkC1ddNor6GNAr6Dj8ZZMrea+V3awbfeRjAk/Vz1IMTJh7OE2M71aiVkVio5Fl5IFT76b8qxZ8OS7bJh3bhePTNEeNKPcQvqzs8NTe22YDfMkgBCitOAjdxPSm61t232ExS/UuabapufP72kIownBfa8kQyy/v/V8Fk2qQpfOquS4Lrlu9TvMXv02/7L+z5aodd75p2d4Ym7dsD1rmq6bR8FuMNmPLQSWSNZMBX7wNx9wuDmZsTPv/NMd07qiCd31eGYasHl9RDtu2mI0vLM37FqxZWdG/RXVs0ahKD4Rl2dNNK530YgUheBzqV1VjOyoXD0j64UQK4EKIcQNwHXAzws+ejfAScC5cmYNIb+zkGfDO39L2d4Uu9Y3RTipdxCfJlj8Qh2PXXuOo4Xp1YS1bNvuI9z3SrJOiJsnJqFLdF06hjdcy8FrztatVxNcM2FYRvpwr2DyNnELb5hpXdkyj8x9edpxzxYjKyi9QV/I5+GZ+ROIJfQeWRpeoTgRcHvWqO9a9yQhZUYWZMjvISE7KbVXSnmfEOIi4BhJ3ci/Silfa88BhRAjgHW2RacB/wpUADcA9cby/2f0wEEI8UPgeiAB3CSlfMVYPhF4EPAAP5dS3mMsHwY8DfQDaoGZUsp2ldpM1zaYotRX6w4w96tDeXrOeHRd4jUEpd7Rg3nxvf0phkv/Ur9Vk+NIOMrSadVseOdvLJs+2nJhmsZMSSAzdcrv0VzdYzvrm2k2uu2mf8GFEFxcNYCpNYMtsdHG2t2uuf9eTWR4XxZu3M7q2WMBXMMbQV/SQ+GWeTSgPMCiSVU8/uYu7p5SXfDfoD3GQ1uCWoVCUXzMN+n00K6qM9I90SW8vP3vTBszxOrau+GdvzFzwrCC952rgHWJlHIh8JrDsryQUu4Azjb24QH2As8Cs0l2Br4v7dhVwHeALwOnAL8RQpxhfPwz4CJgD/C2EOJ5KWUdsMTY19NCiBUkDZnl+Y7VxNQ21DdGmLLsDWuyfeuTI4w/vYnTBySzWzyetot0VYT8DOwVZPzplYR8Gr+8YTy6PN5a2+PRLC+AXaNRWRbI+FKbeoz6poijmNPvEdx4wfAUg2fZ9NH4vcIx91/HOXRkhqQ21+3PMKBWzKihb0nSQ+FUy+P2S77EkXAMv0fj9ku+ZAlo8+k+bP8b5Eq6cNejUbAIVqFQ5IfQ4OSKIKtnj0UTycnM60kuV3Q/Qj6NSWedmtK1d/n00Z2a2nsRkG54XOKwLF8uBHZKKT/NoiWYDDwtpYwAu4QQHwFjjc8+klJ+DCCEeBqYLIT4K3ABcLWxzuPAnRRgjJjYwxBOglLzTTvb5KZpgqH9SikP+lwNFrtBc6WRmWNP7R3cN+kRMYWh5tjSicR1R/HYujnjuW71OxkejHVzxjt6UhJSsnjySIYPLOMnv/7flLSuhzZ/wN1TqjMyZHRd56Atnda8Pk4eira6D+eLk5B25YwaK7PHRGXQKBQdi9ThUFOU7z/9J+u7+OB3ziZUEWp7Y8UJRzQumZ82p8x/8l1+NbdwQXJbXXvnAwuA04QQ220flQNvFHz0pMfjl7b/3yiEmAW8A9wipWwg2Zhvq22dPcYygN1py8eRDM0ckVLGHdZPQQgxB5gDMGRI26127GEIJ0HpDWveYd2c8W2GEcy3fPPtfd/RcMo25ud7G1pSJs9tu48we/XbbJh3bkaJ93RjTtela+let+ZVmsDRkxLyCUucO7VmcErXXoA7LsvMkKlvTJahT78+7ek+bJ5PrkXPHEv4G0XmZq9+O+W6ncgZNPnen58Xht7+Yl7rf3LPpR00ks83udyfcV1ahggkv4vff/pPqmtvNyWa0KksC6S8kK7YspNYonBBcluekaeAl4H/D7jdtrxRSnm4kAMLIfzA5cAPjUXLgcUkM3YWA/eTFMp2GFLKVcAqgDFjxrSpwLGHIdzEnHsawtzyqz+3qUfIpZCXmwZjYK8Aj117jhVi6VPqSxGGmvuOxBKO26eLykYNruCmC4eTkPDwbz9MudEe/u2H/OtlX2bpK+/zat2BjHRdtwwZNzFr3KX7sHk9nTwV+RY9czv2sP6l1nl3hwyafO9PhaIzyeX+jOvScfJSXXu7JwGvxp2XV3G4OQYk9Yx3Xl6Fv6PLwUspjwJHgasAhBADgCBQJoQok1L+Ldv2bXAJ8K6Ucr9xrP3mB0KIR4AXjP/uBewNWAYZy3BZfohk1o/X8I7Y1y+I9IyMx649h4c2f2h5CczMmVz0COlv75VlAT472kppwEPI56Vfqd8xi2T17HM40BhJKSL0wBVnpfQGMPf95HfHOYrHAl7NErDadSnLp492zKY5Go5xzYRh1DdG2bb7iOXJWPxCHfd/+yzHDBk3Q8pNXW+KY508FblcK7tR4nbskoCnKE33egr5ehgUinwJeDXH2kTFmLwUnY8GRNP6rD1wxVk51whpa99tIoS4TAjxIbAL+D3wCUmPSSFchS1EI4Q42fbZFOA94/fnge8IIQJGlsxw4C3gbWC4EGKY4WX5DvC8UQ/ld8A0Y/trgOcKHCtwPCPjipV/4B+WbmHRc+9x28QRjBpcYU3cK7bsBNrWIzjpTxY99x5fu3cLU5a9wY79jcBx/cgbC7/OswvOo1fQl+H2vHn9n4kbKb71jRFaonEr7ffeTTtS6obcu2kHUkpLwPofV5xlPSiCPo9jNo3fo6XUC9nTEObMk8pZPHkkQZ/m2CTJXtcDjuejP/ibDzPy1JdMrWZj7W5XT0Uu18reNdLp2I/MGkP/0gCV5QFO7VNiaVwUCkXHobu0nC9Gl1dF5xPTpZWFCcfnn1gndu29CxgP/EZKOUoI8XVgRnsPahRNuwiYa1t8rxDibJJhmk/Mz6SU/yuEWA/UAXHge1LKhLGfG4FXSKb2Piql/F9jXwuBp4UQdwHbgF+0d6yQqldI1yLcumE7T88Zz56GMFJKbr/kTEv4mU2PkIv+xPSs2L0r6ToSc/1YXLdCGYsmVVkaj/qmSIa+JJaQloB1nTF2gKZI3HHf5vKKkM/aRzSuM3v12wzqE+KZBRMyzs8uZg3HEuw80MS9m5KhnQ8PNLF48ki+OKAMj5bMprl7SrWrpyKfa5V+bOUFUSi6jlgW3Zqi++GmNyxG2C1X70pMSnkI0IQQmpTydyR71bQLKWWzlLKfEQYyl82UUn5FSlktpbxcSrnP9tndUsrTpZQjpJQv25a/JKU8w/jsbtvyj6WUY6WUX5RSftvIxGkXpl7BTOl1+kMIoCzg5dYN27ly1VYWv1DHTReeQR9j8nbC/vaeT68Un9HC2Y6p2zANpRVbdrJk6vFaJnYPwbLpo0nYqr+a4RGAA40Rx32by811l00fzSOvf2yNM+ZSTdEUs3oEzF79thXOMoW4moBTKkIM7B3K6qloz7Uyj628IApF1+FWqdqjvo/dEo/L37MYz9dcPSNHhBBlwOvAk0KIA0BzwUfvBtj1Cm5Fv4QQGb1e5q2t5ZkFExAIx7fz9Lf3XHuleDXBz64exeHmmCVg7VvqQ4jjBoZZufWWi89gQHmAX94wnnhCJyEh4BUEbJ4G03BZuHG7VSY9vZbJ42/uYuWMGvqU+lg9eyyrfr+T9bV7so7TjpuGI9dMlvZeK4VC0bUEfRrLp4+20kHNuhTBItSlUHQ+HVnELldjZDLQCtwMTAd6Az8p+OjdALtewT5x2zMyPALHt/WWSIIZv/hjyrr2DBB7im+u5c5jcZ3WWKqA6P5vn4VGqjB02+4j3P7MX3juxgnoEqQUBDwaA8qSXgLzeNt2H+H1Hft5es54Erok6NXYMO9cogkdjxBoAu68fCQlfo1ITAckl3zlZKbWDKIlmuAL/UrazEhxK+feJ+SjvjGSUyilPddKoVB0LULAKX2CrJsznrieLO4Y9Gsov0j3pG+Jn2Pl8ZSCmf3LA1bhy0LItRx8M4AQohfw64KP2o2wv9WbHofFk0dy+oAyQr7kBHqoOer4tr7rYHNWbYNJPhqHhIRbfpUqILrlV3/mV3PPdZykj7bEMwqPjRhYnlGc7DtGcTVznYBX4+pHUw2pL/YvpTESTxmPLt1742Q7vz4hX7vKsys9iELRffAIONAUY8/hsDV5DeobYkCZewhbceLi83kY2qeEEp/HMi4HlAXw+Qr3TOdaDn4u8G8kvSM6IEgKTU8reAQnOOlv9WbDu0EVx+NkTm/+K2bUkNB11l4/Fp9Hs/Lr3TJsci13Ll26/epSZkzSHg0uf/h4+XqnlNhDzVHH4mSLJ4/M2K53yEtLNJHilVk6rZpeQR8DegWzjjv9/OobI+0uz55vaXiFQtE1tMYkR5qjGamgvQJeenf14BTtwufzcGqfkqLvN9cwzQ+AkVLKg0UfwQlOLm/i5jrPLJhASyTBroPNrHnzE6aMPpXbn/lLysQd8rffgtR1iXBpmOf3ejImaXvmjVP5+pUzaygPeB2NmxJjnPbtzNoiTtlE+eJWmEyVZ1coeg5xl1RQVYFVkU6uxshOoKUjB3Iik8ubuKYJBMLSiKycWeOYX++UBpsNe1pxQpc8ufUTR91KegM6v9dDyO9h7leHMm3MEII+D4tfSO0r8+BvPuDWb5zp2I+mJZo0CuyptG6ZLO2pGVCoqLWta+Xzang1QTiqQjkKRVfRkamgiq4hHtc50BQhltDxGTpEb0dXYLXxQ+BNIcQfAStNVkp5U8Ej6EHY3/bdJm63NFg75h8bJA3NMeYamTpmdstz2/ayaFIV/Ur9nFIR4iQjRJJeMv2XN4xj0tmDmL36bdfqqn5vamffi6sG8KNLqwB47Npz6F/mz0gDTjcggi7xwmz9ZNxEre0VojqVjF86rZp7NyW7GueiR1EoFMXFqwnHlx2V2ts9icd13t/faGWPmpKEMweWF2yQ5Lr1SuC3JBvW1dp+FDbMt31Ird9hYv6/vjGS4U2Ix3X+fiTMgWNh/rq/kStW/oG/7D1mGSJwvCLq5WefAkBClyQLzjo3h4vEJfON7d2qqwqhWYbIqMEVXDNhGNN//kerwqwmkg8TOJ5NlFLZdOYY+pc5N7Yz67Oct+R3GZVS7eEvs7psIcaC0/nfuiFZNdbUoxxqjrZr3wqFon0EvBo3XjCcxS/UWTWYbrxgOAFVDr5bcqAp4ljGIvnyXBi53hE+KeW/SCkfk1I+bv4UfPQehr04l1mzI70c+o1PbcuYmE1r84qVf+BoOG4ZEG7elZMrQtaX+8pVW9mxv9FRg+ERSfHpypk1eD0i5fNRgytYNKkKKSWLJlUxanCFY3XTuWtruf2SLzGoT4htu4/w+Ju7WHPdWF6/9fykAXGSswHhZBykGwTFLEzmpkExq8YqPYpC0fm0xnXrZQeS38MFT75Law4eYsWJR8yl0Wm8E7r2mrxstIv+NalhmoI69/Y00sWuIb+HZxZMoDWmp5RDB1IyR+zWpkc7bjS4hUX+dqglY5JfP/fcjHWDfo/VpMosEW96QNLFrEumVlPi9zjeaI2t8RStyT0v/5U7LvtyVh1NZwtU3TQoR8Ix63dVGE2h6Fx0F82I6k3TPfF5NMfnrNdTuKcr1z1chaEb4XiI5p2Cj97DSejQvzRZDv2hzR8y7/zTWTdnPCtn1lBZFrAmZru1mdCl5U1xCousmFHDQ5s/TDnOnoYwHkFGczipSx57YxeLJlVxSu8gP7s6WRreyQOycON2ygJex9BSedCb4madfd6wNrOC7CEr+746yiBwa8y3YstOVRhNoegi3MrBe5VmpFsyoCzAihk1GXPSAIdQfb7kWvRsWMFH+hzgJKJ8ZNYYTurtd2yjHfQnbUHzC7unIcymv+xj+Ywa5q+ttcIiT353HB4tWcbdo0F9Wnwu2RtAy0hBjicSKaLVuV8dyi9vGI/uUqsk6NNYNn205VY1b7SgT+M/rzybyvIAR8Mx+pX6aWyN0xrTXZXUxRaotkW6V8rMpnn46lEqm0ah6CKEgPu/fZZVqNGsGC2UZKRb4vVqnDmwnPVzzyWe0PF2VjaNEOICKeVvhRDfcvpcSvlMwSPoQbjpJNbNGe+Y5vuruecCUBb0WAbIGSf34qebP0gJi9z9Yh13T6lusxx6egry34+ELUNk1OAKvjZiIFc9sjUlZGMyqE+Iun2NrNiyk8WTRzKkbwkf1Tex6L/eY9vuIwzqE+K/FkwgmtD5YH+TVU2xpW+coX1LM27GrqiU6piCXdphh1MoFG2gCUFFiZfVs8eiCdAlJPQEqiB898Xr1TilItT2ivnut43P/4FkFs1lDp9J4HNhjGRLUbXjppNwy7WPJXSrN4tpgAwfUMardQd4te5Ayvp3XJYM6eQzyds9IPbQjFOPnSVTq7nvlR1WR93f/eB8q8CZme4b1yUHGyM5V2BVlVIVCsXh5hi3bqhNeWZUhFTIVJFKVmNESnmH8etPpJS77J8JIQoK3QghPgEagQQQl1KOEUL0BdYBQ4FPgCuklA1CCAE8CPwjyeJr10op3zX2cw3wY2O3d5lZPkKIGmA1EAJeAr4vzTzYPHALvTilobqJKO1hGPtyTRNMWfYG93/7LMsAWTmzps1iYG6TfLrRpNmqtdozc8weO4smVXHmSeV8XN9sGSLm8Ur9HtbNGY8m4FBzjOk//yNPXDfW0cOTSwXWXA06hULRc4jpst3PDMWJSUc9y3MN9Gx0WLah4KPD16WUZ0spxxj/vx3YLKUcDmw2/g9wCTDc+JkDLAcwjJc7gHHAWOAOIUQfY5vlwA227Sa2Z4C5pKiaOIkoH5k1xlH0s3xGDU+8uYs9DeGUmiSOtTxy0Fo41fWQUnL/t8+yskrsQrJtu4+w+IU6DjdH6F/mt3Qopk6kb4mfU/uUIBFWpk/CrS9OG8p4XZd8cqiZ9/YeZU9DmPf2HuWTQ81KUa9Q9HASKpumR9GRz/K2NCNnAl8GeqfpRnoB2TujtY/JwPnG748DW4CFxvI1hmdjqxCiQghxsrHua2aKsRDiNWCiEGIL0EtKudVYvgb4JvByvgPKlqLqZCG6hVDSRT9+j2Dlf38CkBI2MUWrTxmiVfs+slmkTkbToeYoQZ/G4skj6V/mzxCnJiuwenjwN6kalYc2f8Bd3/wKA3oFUzJ9PjvamlcFVpMj4Sj7j7VmhHcqSnz0LVVhHIWip9KRqaCKzqcjn+VtaUZGAJOAClJ1I40kvQ6FIIFXhRASWCmlXAUMlFLuMz7/DBho/H4qsNu27R5jWbblexyW541b6CXk97iGb8wQSrrxcFKvoGU81DdGrP2aYZPFk0dy+oAyQr5M11db4SIno6ks4GXWo29Zy0cNrmDx5JGcVllqhWYeuPJsR43Kjy9NalTsIab7X/0gQxnvVoHVTjiacHTVrpszXglMFYoejeQ/rzybf173J+uZ8Z9Xno1AeUa6Ix35LG9LM/Ic8JwQ4lwp5R8KO1QG/0dKuVcIMQB4TQjxftqxpWGodBhGIbc5AEOGDHFcxy1FNa5Lx/CNWcisLeMhfb/1TRFO6h1kUEUowwg51BwlHIvz2dFWKssC7GkIZxzPyWgyx2ViilN/feN5lPg91DdF8GTRs9Q3RvB5RUqq8S/+52Oe/O44NCEIOhhNTnRls6zurFXJ5f5UKLqKXO5PKWHV6ztTPK+rXt/JHZd9uTOHqigScV1SWRZI+Xuu2LKzKM/yXCuwThFC/C8QBjYB1cDNUsq17T2wlHKv8e8BIcSzJDUf+4UQJ0sp9xlhGPN1fS8w2Lb5IGPZXo6HdczlW4zlgxzWTx/DKmAVwJgxYxyvplv2yr6j4awVRt20JqbxkEtWjJNBY896sR/PyWgKeJ1dpEfDMe5/9QMWTx6J3yNYOq06owaK1xDX2uuTxBM6CQmagFPTjKZsdJWrNptBCJzwRkou96dC0VXkcn96NcENXz2Nm9cf96Y+cMVZquhZNyXk1bjz8ioONycrW/s9yf8Hi1BnJNc9XCylPEYyZPMJ8EXg1vYeVAhRKoQoN38HLgbeA54HrjFWuwZ4zvj9eWCWSDIeOGqEc14BLhZC9DGEqxcDrxifHRNCjDcycWbZ9pU3Tj1U2qowmks59LZ6szgZNAs3Jpu/pR/PqfFc0Kc59sfxaMLyxPQt8VNZHmDx5JGsmzM+qS8pD/DY/3xsHXflf3/CVY9sxefVKPF7OLmXuyGi65L6xgh7G1qshoBeTfDAFWeljKMzHkhuBuGRcDRrEz+FQlEcfF5BRak/5flSUerH51XGSLdEuPzd3JbnQa6eEZ/x76XAr6SUR0VhBx8IPGvswws8JaXcJIR4G1gvhLge+BS4wlj/JZJpvR+RTO2dDcneOEKIxcDbxno/sfXLWcDx1N6XaYd41cTJ1d9WhVE3rUku5dDN47VE444GTUXI55hlk57yu7ehhXs37Uhxqd27aQcPfudsnl1wnuUNGNq3lBK/11Fcaz/u3oYwt/zqz66pzW6eiL4lPv79pfdTxvHvL73Pw1ePynqNC/VUuBmE4Wgiq9dKoVAUh8bWBNs+OcyE4ZUkdIlHE7z5YT3jTu9PX6UX63ZIKWmJJjJrwZ6sAAAgAElEQVQErO2ompFBrsbIrw1NRxiYL4SoBFrbe1Ap5cfAWQ7LDwEXOiyXwPdc9vUo8KjD8neAke0do0k2V3+2MEsu5dCdJmDAOt6iSVVcXDWAqTWDrUl8Y+1uBvUJpRgTTvsL+jWEEPzo0i9xqDnKPS+/b1VSDfo9KZNuekU9u7jWxEwPzjZxu3ki1s89l8ry1NTkynK/ZZjlU8slH9wMQrcUZdXVV6EoLkGvxrDKMr6zamtKmKYYbn1F59ORdWNy7U1zuxDiXpLhkYQQooVkum2Ppy3th9ubdFuaELcJuF+Z31q2uW4/N14wPCUdd7nRlMiXlk5r5n9/eqiF/mV+ZDMZabyPv7mL2ecNyxoeicd14gmdJ64fyycHW3ho84fUN0UsrYp5DZwm7nRPxKjBFcw7/3RiCZ0fXVrF3S/W8WrdAes8BMmQjiS7GLi9OBmEK2fW4BXC0chTXX0ViuIiwdKLQPK7ffP6P7Nh3rldOzBFu9ClZMJp/bjha6fh0QQJXfLI6x+jd7RnRAhxm5TyXuO/F0opfwUgpWwWQvwI+H8Fj+AEJxfthxvZyqG7GTlP3TDOWnZh1UDLoDDXmb+2lvVzz83oDWDP/140qcoq5W5ut3Djdp66YTzf/+W2ZHjEwUUaj+u8v7/RKnJmFkALRxP8+0t/TanQ6jRx2z0RowZX8INvjMgoOV/fGGXb7iPMX1trjXPt9eM6xFORbhAmdMldL9bxlVN6808XnsF823kun1FDRTBXR6GiOzH09hfzWv+Tey7toJGcWGPpDKJx3eW7rXfRiBSFUB7wMOPcLzB79dvWs3PZ9NGUBwp/kWvLV/Yd2+8/TPusXRVNuxttCVXbi5uR4xHHW27bS7jb14knMr/I9vxv+3ajBlewcmZNslMmqeGRdA40RSxDxDzWvLW1DOgVSKnQ6hRuSopVdaucvb0Xjrkvu/h2T0OYU3oHWTQp2fPmsWvPYdTgCmuf+ehr0gWzdkyD0O/1cPXP/8irdQeY+JWTLUPEHMv8tbXUO1TVVSgU7ccsHWBnUJ8QHpVN0y1pieoZL8gLnnyXlmjhxmVbr4LC5Xen//dIctF+tIdsxdTM45kl3HNJibXrIMztKssCGd6JFTNq6BPyZWwPpFRbNdnTEEZAzuGmi6sG8NR3xyHBcV8VxrEvrhqALrE8OKYQ6t5NO6hviljXOJuwNRetiV0MvGhSFSu27MSjiZyNPIVC0X58HpFR+XnZ9NH4PJ+L6aPH4VYzKt4JdUaky+9O/++R5NMlNx/cjJyKkJ9eAR/r554LSFbOqGFuWthkgEPF06DvuHFjlpePxvUM78S8tbU8s2ACA8ozq/lnqweSa7jp1boD1O1rZP3cc11FsIP6hLj9ki+lVIc1hVDr5ox3FPM6GRtt6Xnc6rSYY+nsuicKxeeNWELy8G8/TMmke/i3H6qiZ90Ut6avxSjT0JYxcpYQ4hhJL0jI+B3j/x3Rm+aEJNcuufkYKW5GDsCH9U0pnoYnvzsOAXg9GgPKAngdlOj9SwOWcWP2t/nRpVWOVmxrzNkDYDb0S9eMOBk/Ju7hJhzFo/1L/Tz13XE0tMTarOTXlrHRlp7HrU7LT686O+Ntra3zVCgU+ZOQ0rndxKSqLhqRohB8HsGj145hb0MrJX4PLdEEp/YJFsXT1VY5eJVe4EJHpaO6eRrayixxMm5i8YSjFet233i9WkZDPzfjx8Qt3KRpmqtHKR7XCXg1fjL5y8y3GQRLp1Wz90jSQ2LWJ8lmbLRVy8XNWOlXGqBXyJvXeSo+P+QjMu3uAtOOxtTAZT6DVJimO6JLaI6k1hn56VWj6BV0Dv3ng3r6thO3t/ZDOYogTWMmswqom/o8kbKtk2gzvaJr0O9xrMAa8rvbmGbNkSH9SjmlItTmBG2Gm+zHMPUe9vH0K/VzqDnK/qNhdhxopG5fo2WImOd464btVsvxG9a8Q0Ji7dcU4m6Ydy5CJDsYZzs2uIuPQ34vvYJ+fB4NjybwebQTrhS8QtETCHg1lk0fnfIdXTZ9NAFl+HdLpIR/+uW2lOf2P/1yG0XI7M256JkijUJSfnVd8tmxVtcCYdne9vPxyFSE/AzsFWTx5JGU+D1oQnBS7yDhaIIDeiteTRCOFqaDybfHzqJJVWys3c1tE890vH4+Q7expyGMlJJHZo3hgdd2cM2EYSlC3LYKz+m6RCJZe/04dh1stuqlPDJrDH1Cvg7xaikUilRaYgl+//4BnrphPLqUaELw3Lt7+ObodjVRV3QxbkkOsSKI/5Ux0k7yLfdu15ckdOmqmZBSsua6sXx6qMWKyX2hX4n1tt+WjsKOpgmG9iulPOhD13UONke56pHjlRDTs1faOxnbNTX28wz5PcR1SSyuW2M+pXeQayYMY/fhsKvA1X4tRwwMceflI7li5R9czzn9vJ0MtpUzaji5IkhFyJ/XNVQospFv3ZDPGwGPxphhfbk67bnjV2Lxbolbl/dipGqrO6KdtBUisJMekrn653+kb6mP2yaOYPELdVy5aiuLX6jjtokjCHg1wrFkTO7KVVtZ9Nx7RGwFgrJ5ZJzCN6ahoGkac59Ira1x64Zk3Y98Q0xu2M/zxqe2seOzRr617E32NBzvcBz0eVi4cTsPbf6QJVMzQ0grtuzMCPXIPMu3Oxkbc9fWktCThlMhXi2FQpE7CelcPjxRDL++otPxasIx9N8Z2TQKF/JJ+XWaHPceaeWxN3aleEYee2MXCy/5UobRYH9rd/PI+Lxa1tCD2wRs1v3INhnnmjVkP89Fk6qsh5C9XkpTJG4ZJ/e9cryJ36l9QpT4PTx89aiMY+TrhWrL2CikiaFCocidWMKlLkVCGSPdkUhcd22+WijKM1IA6YJRtxCH0+RY6vdwzYRhKZ6RayYMQxPOxcLMidTNI+PVRFZBrZuYMz0sko670DbzYWI/T3sVWLPuyaA+IQ4YTfgAtu0+wtwnarnlV39GE4K+pc7XMh8vVLZz9Xk16hsjROMJnvruOC6uGpDT/hQKRftwq8CqtFndE68mqG+KMPeJWq5ctZW5T9RS3xQpimdEGSMdiBk2ScjMcuchv9exXLpH0xy/vJDspgtYHpk3Fn6dZxecx4iB5YSj2b0BThO6U1gknXyyhuxGgOkNgaTRcd8rO1g8eSRfObUXK2bUpIxjxYwavEbKrxN2L5T9nN0eaG7GS1NrPCVU9v3/ewZ//OEFbe5PoVC0D7+LW9+vvmvdkpBfc3x+h/yFmxIqTFNkzJCGKRg1Qy5mSpsADjZF8XmcS5K3RGIsmVqdkjmydFo1Nz61LUVomi609Hmdq6f6PMe9AQN7BXhmwQRicR2fV8OrCcewiJ189BX2qrIrtuxk6bRqK1RT3xTB79U41BTliT98yprrxiIEfHKwhUX/9R71TRFWzKjhzIHljunE2ZoOOq2bHkLzaHD5w2+k6kieqFWiVYWiIxHQv8xvZfS1RBP0L/N/TpqJ9DziOpQHPayePRZNJOuO+DzJ5YXS6caIEGIwsAYYSLKk/Cop5YNCiDuBG4B6Y9X/J6V8ydjmh8D1QAK4SUr5irF8IvAg4AF+LqW8x1g+DHga6AfUAjOllEXpgpZrrxSnzrkLnnzXWv7Ud8c5Gg+fHg6zsXY3T313HAjYeaCZezftsDrmumV9mMIic/I3jZiErvPtlceV7BlZMw7de+3ko6/QNMHwyjKrmNj+YxHu+dZXOKl3kN2HkxqReeefzpsfH+LCqoEp1wdgnktH4nz+Bm605TlSKBTFJ5aQbHhnN9PGDLFazm9452/MmjCsq4emaAeRuM70n7+VMR88PWd8wfvuCs9IHLhFSvmuEKIcqBVCvGZ89oCU8j77ykKIKpLdg78MnAL8RghxhvHxz4CLgD3A20KI56WUdcASY19PCyFWkDRklhc68LZqfNhDGm4dd83ld71Yx8qZNSmeE7Nc+ughfehX6mff0TCzV7+dsQ+nCTQcTaQIi3QpSeiS1rjOY9eeQ2sswd+PtvLAazu4e0p1zt6AfBoF6rq0Stnf/+2zuHLVViBZsOwH3xiR9H4YHhOfR3MRtmU3sXNtjpe+jpvxp0SrCkXHoQn42oiBKS3nl0ytRlMCgW6J7tIoTy9CdlSn3xJSyn1SyneN3xuBvwLZKuBMBp6WUkaklLuAj4Cxxs9HUsqPDa/H08BkIYQALgA2GNs/DnyzGGM/2Bxx1E8cbE5qOewhDbtmwsQuGH217gD9S/0pOogvndSLgb1DloDTTYjpNIH6vR5LWHTPy++jS7j9mb/w9ft+z+zVb3OsNc7G2t1cM2EYup67Ty0fvYbdGHPTjDx01SiG9ithYK+g47m11awuFw2L0zqm8ZerCFahUBSOLnHUxuXxCFKcQLgJkotR3r9LNSNCiKHAKOCPwHnAjUKIWcA7JL0nDSQNla22zfZw3HjZnbZ8HMnQzBEpZdxh/YJojTm7+lujCeobIym6DTODxPwiXlw1gNsv+RJHwzFWzqxhY+1uNM29Gy7k55Wwrzvv/NMdHwCLJlWxcON2oyNw7uSq17AbYyu27OThq0fR0BxLqf6qCfB4NEoCguUzapjv0JQvWxgmFw2LfZ1RgyuYd/7pVIR89An5eP7G8wquOqtQKHIj4fImnXDIxlOc+AgBj107BiE0SzMipU4xWg11mTEihCgDNgL/LKU8JoRYDiwmqSNZDNwPXNfBY5gDzAEYMmRIm+u7NX1K6JIpy95gzXVjMzrnPvXdcQS8GvVNUWY9+lbKxKvrOvWNEddJMZ9aJvZ1W6Jxx8l4QHmAyrIAsoMKDvm9HuZ+dSjTxgwh6NOIxHXLGJGQUv31kVljOHNAWUazOk0TmdVTjfCVpmmuQl27t8j0KFWWBfjBN0Y4lpHvDkZIvvenQtGZ5HJ/ejRhPRPsmpFiVOxUdD5Bn8ahZsn8tcfnsuUzauhXVniQpUsid0IIH0lD5Ekp5TMAUsr9UsqElFIHHiEZhgHYCwy2bT7IWOa2/BBQIYTwpi3PQEq5Sko5Rko5prKyss1xB/2aY5rakXCUPQ1hZj36FgN7BayQxl1TvkJZ0Etcl8xbm1rIbN7aWv6056hVtyMe13NqfpdtEjXXLfF7GdQnZGk1zFomMx99i9smjrD6vxSbiqCXSWcPsuLD9Y0RFj33Hn8/2sqCtKZ4N6x5hyOtcasp30m9gjSEY+w50sJnR1upLAtY68594vi1amqNt1lzxPQS3XTh8AwPUTEqzXYW+d6fCkVnksv9WeLXrGfCBfcnQ8aTzh5ESRFSQRWdTziq89PNH7BoUhXr5oxn0aQqfrr5A8LRbtibxtB0/AL4q5TyP2zLT5ZS7jP+OwV4z/j9eeApIcR/kBSwDgfeIpkcNtzInNlLUuR6tZRSCiF+B0wjqSO5BniuKGNHUOL3pKSpmf9CcrILRxOc2qckRUR5/7fPyipmvWHNOzz13XFc/fM/FuUN3pyMPzvamjEZ37phO+uLoHx2or45aoVdTuoVZKbhCXIT85qhFSfB6ZKp1dz3SjKLyL6PWY++xfM3npfVW2R6iUoDHpVBo1B0IS1R3XomQPL7N39tLevmjKdPG5l8ihMPIchoWrpkanVRwjRdYZ6eB8wELhBC/Mn4+UfgXiHEX4QQ24GvAzcDSCn/F1gP1AGbgO8ZHpQ4cCPwCkkR7HpjXYCFwL8IIT4iqSH5RTEGHo4muPP5OqJGxkc0oXPn83Voxl/CXuXT/oYfS+hZxax7GsIcaIzk/AZv70FzqLmVfUfCfHqomb8fCROP69ZkfFplqXPGSgfFa+0dHRO2fjJuYl5hXDcnwenCjcm+Oea69msVjiba9BZpmiDk8+YsAFYoFMUn7qIZ6ahnkKJjkS6C5GJE/jvdMyKl/B+cS968lGWbu4G7HZa/5LSdlPJjjod5ioYQx0vhmpgTpb3Kp10bsmRqNSVGeMdeA8R88zf30TvkY9TgCqueiNMbvK5LDjZHaIkk2HWwmZf/so8po09N2a+9cJjPpcNiMUr3OuHzHNdzfHa01VXMa56/xxhGtr45TtcqV2MiHwGwQqEoPt5OfgYpOhbdpWlpt0zt7c54BBmdZn929WiqT+3FMwsm0K/UbxkicNxqLA/6rBogzy6YwJrrxvL4m7sAeOzac3j8urEcao5yx+VVVsn49EnXDGV8a9mbnH/fFhY99x7Tx3+Bx97YlaFFOdCUTDUO+j08cMVZKeN94IqzCPo7xjMwoCxglQq+/9UPrGObYt41143l2QUTWDSpisff3IVmFBtwS2E264M8/uYutu0+krcxkW8ZeYVCUVzKQxrL08qHL59RQ3lITT3dEa9LuxJvEQrHqHLweaBpGo+/mdpp92e/+5B7plaz/1iE5kjc0Wr0pHlURg2u4MGrzuZYOG4JWwf1CfHgd87mtokjuHXD9oxJ1x7KMDNkYgmdW79xJvWN0RSPilk4rCLkp19ZIEXj0q8sQEWoYzwDXq/GmQPLrQyZoM/DM/MnEEvoJHTJXS/W8WrdgQyjws2DcXLv5E1/95Rq7risfem4+ZSRVygUxSUckZT5tZTy4R4hCUckvYJdPTpFvlQaL5zz0koymAkHhaCMkTzoV+rn5otGZEyacV1aJeCdXJIlfk9KtdX6pgheITIybL7/9J9YP3c8zy44L2PSNUMZZoZMesjDFHvaC4dpmmBov1LKg768SqcXgterOZZz13XpalS0lcKsjAmFonuSkJKZj76d8UxcP7djRPSKjiX9hdMsyeDUTyzvfRdhfJ8b3CbNfUfDrtqIR2aNobI8SGV5MGU7ey0Qk6RXQ3JKRebkK4waJ9kKmi1+oc4qHGYf84kwmbc1jhNlnAqFonjEEi4C1oQSsHZX3F44C95v0ffYw3GaNE3Ng1n2fNGkKvqV+jmlIsRJvYKOb/h7GhKOXhQ3r4WpVwl4nXu6nHlS0lotlpWqUCgUheJxEbAq3ZYiHTVrFQFT82AaJItfqKM04E0xRNLxe5wLqPldCpKZepXeRoaJnWQoyMspFSFliCgUihMGn9FNPP0551PGiCIN5RkpAvmUbTfpW+LnWHmquLSyPEDfEmdxqalXWfrK+46hIJWuqlAoTjT6hHz0T3vO9S8P0Cfk6+qhKU4wlDFSJPLVPHi9GkP7llLi9+YkBDINnrunVKPrOuvnnouUUjV8UygUJyx+v5cvVIQo8XmI6xKvJqgs9eP3q6lHkYq6I7qQfIVASuSpUCi6G36/l1OV8aFoAyUwUCgUCoVC0aUoY0ShUCgUCkWXoowRhUKhUCgUXYoyRhQKhUKhUHQpyhhRKBQKhULRpQhZhNa/PQEhRD3waTs37w8cLOJwTiR68rlBbud3UEo5sTMG40aB92dH053uke40VuhZ92d3u/btRZ1nKjndn8oYKQJCiHeklGO6ehwdQU8+N+j559cZdKdr2J3GCt1vvNnoSeeSDXWe7UOFaRQKhUKhUHQpyhhRKBQKhULRpShjpDis6uoBdCA9+dyg559fZ9CdrmF3Git0v/FmoyedSzbUebYDpRlRKBQKhULRpSjPiEKhUCgUii5FGSMKhUKhUCi6FGWMKBQKhUKh6FKUMaJQKBQKhaJLUcaIQqFQKBSKLkUZIwqFQqFQKLoUZYwoFAqFQqHoUpQxolAoFAqFoktRxohCoVAoFIouRRkjCoVCoVAouhRljCgUCoVCoehSlDGiUCgUCoWiS1HGiEKhUCgUii5FGSMKhUKhUCi6FGWMKBQKhUKh6FKUMWIwceJECagf9eP00+Wo+1P9ZPnpctT9qX6y/OSEMkYMDh482NVDUChcUfen4kRG3Z+KQlHGiEKhUCgUii5FGSMKhUKhUCi6FGWMKBQKhUKh6FK6nTEihHhUCHFACPGey+dCCPGQEOIjIcR2IcTozh6jQqFQKBSK3PF29QDawWrgYWCNy+eXAMONn3HAcuPfE5p4XOdAU4RYQsfv0fD7BK1RnZDfQ1yXxOI6Pk/SdmyNJfBoAq8mCPoETRGduC7xaoKygEZTRMfn1fBqApCEo8nPe4c8NNvWDfk1GlsTBL0aIIjrOl5NAyQJKZESdCnxezSEEMQSxz9vjev4NIHXoxHXdaRMyqaDXo1oXCemS0I+D/FE8ne/R0MT0BrXrd/NYySM8fi8Gi3RBD5PcuzhWIKAV0MAfq+gxTgP+369mqA0oHE0nDwPXUI0oVvbRRI6HiEQyUuB16MRjiUy9tEv5CcY7I5fh0zicZ36pgjRhJ5y3b2aoMSv0RLVSegSTRMEvBp+DzRHdBAk/x5S4tM0vB5BNJ685h5N4PdoeDRojibQRPL+Exz/O4b8HipCfjRNpIzFvK99Ho0BZQG83tR3oGg0Tn1z1Lovg16NmC6JGve8EBCJ64S8GmiCWFwnISVBrwddSiJxHY8m8GkC3RiL0MAjNGKJ5PiDXo2EhLievB/KghrNrcf//l5NEDGO1zfkoykWpzWW3Nbn0Qj5BJG4TF4LAbrE+sxjXN+gV0NoyWtm3dMeDaQkLiUeIZAkt9PNbT0QM/ab/D5rtMaS929LNIFmXPe+Jf6M66ZQ9CS63dNXSvm6EGJollUmA2uklBLYKoSoEEKcLKXc1ykDbAfxuM77+xuZt7aWPQ1hBvUJsXRaNc++u5cpo0/l1g3bU5bfu2kH9U0Rnrj+HA406cy3bbd8Rg1b/rqfdbV7eOL6c2iKJD+/6eun86VTKzLW/eveIwzuV5pyjJ9dPYrWmM4tv/ozlWUBbps4wnUMbuvms53T56nrjqYk4GH2Y2877nf5jBo+O9JCWdDnerwlU6t5/M1dzD5vmON1XT6jhuH9Sru9QeJ2L5nXYfmMGl740x5W/vcnDOoTYv3ccew/FuehzR9wzYRhLNxouybTR/PT337Iq3UHrP2U+D3c+Xyd9Tcq8XuQwLLffcTs84YxsFeQof1K0TThOJYVM2o4c2C5NbFGo3F21Den3JfLpo8m4BXcvvE96zjPvruX6eOH0BJNZL2/Qn4Py373EXO+djo+j+B7T23LWPfiqgH804VnpBzTfo1Wzz6HcDTB/CffTRl3Qtf52e8+yrhOTuMzP3vgirMo8XvweASRmJ7xefo1Xj6jhtpdBxk9tB9r//Apb358iKXTqjlWHmBo39JubZAMvf3FnNf95J5LO3AkihOR7ntnu3MqsNv2/z3GshOWA00R64ENsKchzK0btnPD106zHlz25fPOP509DWG8msd6oJqfz19by+TRgzI+nzC80nHdCcMrM45xuDlmGQnzzj896xjc1s1nO6fP7b9/76l32XM47Lrf+WtrqTqld9bjLdy4nak1g12v6/y1tRwKRzv8b93RuN1L5nWYv7aWaWOGWJ8ldMG8tbVMrRlsTbDmZ/OffJepNYNT9nO4OZbyNzrcHKOhOWZd208PtXCoOeo6lnlraznQFLHGW98czbgvFzz5Lh7Nk3KcG752GoebY23eX+ZY/nndnzjcHHNcd2rN/9/e/cfZUdf3Hn+9zzm7m80P8osNxSTKD9FKNWCyRcVeLoql+KOiJvJDUkQtFBR/Vnvp1XK9tI9bkVpsH0IoEQuIighVqdLiL5BWlLJBAhJEQkSTVCGGgCQk2d1zPvePmbPMnj1nf57s7Nm8n4/HPnbmO9+Z+czMd85+dma+Z5YOWWd2H21+YvdAIpKN+4l02bX7qV581WkfvGE9jz/dS6lQrDu9dh+fd906Xn3kwbz7C/dw9nGHDSx/8xO7B+03s+mmtf8NnCBJ5wDnADz3uc/NLY6+cmXgA6pqy47dFAuqWz6vsw1ILo/Xm55cFBo8vVypX7de+cz24kDZvM62YWNoVHcs89WbXjs8s7047HL7G2xf7fKG26/9lVF/P8+kGE/7bNSWsvuhmLmNUm0jIx2v6vjM9iIzKQ4aB5hJcWC8t788bCz95crAeKPjVhBDYh5Nu6zGN1ybGW/bzC67dlptfLXzFTRym6+OR3pMqsepuozsfpsKpsrnp00P0/HKyFZgaWZ8SVo2RERcGRHdEdHd1dU1KcHV01YssGR+56CyJfM7KVeibvmTu/sAKEp1p0saMr1YqF+3XvkzveWBsid39w0bQ6O6Y5mv3vTa4Wd6y8Mut9Rg+2qXN9x+LWX+SE8F42mfjdpSdj+UM0lXtY2MdLyq48/0loccl2pZdby9VBw2llLx2Y+dRsetEgyJeTTtsjaWenXH2zazy66dVhtf7XyVGLnNV8eVHpPqcaouI7vfpoKp8vlp08PUat3NcTNwZtqr5uXAU1P5eRGARbM7uGL1ioEPqup96LV3bOKSVcuGlF9x+yMsmd9Jf6XMmpr51qxewdfv2TJk+p0Pb6tb986Htw1Zx4JZbXzqrUcl98pvf2TYGBrVHct89aZnhy9723KWLOhsuNw1q1ew4b+fGnZ9F69cxk3rNjfcr2tWr2BhZ/s+P9b7WqO2VN0Pa1av4MaeXw5MKxaCK1av4KZ1m7l4Zc0+OWM5N63bPGg5C2a1DTpGC2a1MX9W28C+fd7CmSyc1d4wlitWr2DR7I6BeLtmtQ9pl5efsZxypTxoPWvv2MSCWW0jtq9qLJ8+9WgWzGqrW/emdZuHrDO7j5YuSLa9Nu4F6bJr91O9+KrTLj3lKBbNaae/Uq47vXYfr1m9gu9t+BWXn7GctXdsGlj+0gWdg/ab2XSj6iX9ViHpS8DxwIHAY8D/AdoAIuIKJZcFPgOcBDwDvCMiekZabnd3d/T0jFhtn6n2OuhPex20Um+acqVC9Z/tjvH0pomgpKG9afb0lWmfYG+a3nKFwsR70+R+yWQs7bPam6bag6Vub5oIChpdb5pqz5tGvWkqEVRG6E3TX65QmkBvmt60t0q93jS9/RUKQ3rTiGLaZsuVoGMf9KYpV4JSg940lbQH0si9adLtSeuPszdNS7RPP8C63xpV+2y5Z0Yi4vQRpgfwnkkKp2lKpQLPmTf4Ei6zRjfv3DYGhroAACAASURBVJnDj2eXM69m2oJRrmMqmD9MrLXbtT8rlQocXNuWMurtxyFtZhgLxxjLkHZdo729xOL2yf8omjtMWB0dLffRaNbSpuNtGjMzM2shTkbMzMwsV05GzMzMLFdORszMzCxXTkbMzMwsV05GzMzMLFdORszMzCxXTkbMzMwsV05GzMzMLFdORszMzCxXTkbMzMwsV05GzMzMLFdORszMzCxXTkbMzMwsV05GzMzMLFdORszMzCxXTkbMzMwsVy2ZjEg6SdJDkjZKuqDO9OdKuk3SjyXdJ+l1ecRpZmZmI2u5ZERSEbgMeC1wJHC6pCNrqn0MuCEiXgqcBlw+uVGamZnZaLVcMgIcA2yMiE0R0QtcD5xcUyeAA9LhucB/T2J8ZmZmNgalvAMYh8XA5sz4FuBlNXU+DnxL0nuBWcBrJic0MzMzG6tWvDIyGqcDV0fEEuB1wOclDdlWSedI6pHUs23btkkP0mw4bp82lbl9WjO1YjKyFViaGV+SlmW9C7gBICJ+CMwADqxdUERcGRHdEdHd1dW1j8I1Gx+3T5vK3D6tmVoxGbkbOELSoZLaSR5Qvbmmzi+BEwAkvYgkGXHqbmZmNgW1XDISEf3A+cCtwIMkvWYekHSRpDem1f4cOFvSeuBLwFkREflEbGZmZsNpxQdYiYhbgFtqyi7MDG8AXjnZcZmZmdnYtdyVETMzM5tenIyYmZlZrpyMmJmZWa6cjJiZmVmunIyYmZlZrpyMmJmZWa6cjJiZmVmunIyYmZlZrpyMmJmZWa6cjJiZmVmucvk6eElvGW56RPzLZMViZmZm+crr3TR/nP5eBBwLfC8dfxVwJ+BkxMzMbD+RSzISEe8AkPQt4MiI+FU6fjBwdR4xmZmZWT7yfmZkaTURST0GPDevYMzMzGzy5XWbpuq7km4FvpSOnwp8J8d4zMzMbJLlmoxExPmS3gwclxZdGRFfzTMmMzMzm1x5XxkBuAd4OiK+I2mmpDkR8XTeQZmZmdnkyPWZEUlnAzcC/5QWLQa+Nor5TpL0kKSNki5oUOcUSRskPSDpi82L2szMzJop7ysj7wGOAe4CiIiHJS0abgZJReAy4A+BLcDdkm6OiA2ZOkcAfwm8MiJ2jLRMMzMzy0/evWn2RkRvdURSCYgR5jkG2BgRm9J5rwdOrqlzNnBZROwAiIjHmxizmZmZNVHeycj3Jf1voFPSHwJfAf51hHkWA5sz41vSsqwXAC+Q9ANJP5J0Ur0FSTpHUo+knm3bto1zE8z2DbdPm8rcPq2Z8k5GLgC2AfcDfwbcAnysCcstAUcAxwOnA2slzautFBFXRkR3RHR3dXU1YbVmzeP2aVOZ26c1U95deyvAWpJkYQGwJCJGuk2zFViaGV+SlmVtAe6KiD7g55J+RpKc3N2cyM3MzKxZ8u5Nc7ukA9JEZB1JUnLpCLPdDRwh6VBJ7cBpwM01db5GclUESQeS3LbZ1NTgzczMrCnyvk0zNyJ+C7wFuDYiXgacMNwMEdEPnA/cCjwI3BARD0i6SNIb02q3AtslbQBuAz4SEdv32VaYmZnZuOXdtbeUvhzvFOCjo50pIm4heb4kW3ZhZjiAD6U/ZmZmNoXlfWXkIpKrGBsj4m5JhwEP5xyTmZmZTaK8H2D9Ckl33ur4JmBlfhGZmZnZZMs1GZE0A3gX8HvAjGp5RLwzt6DMzMxsUuX9zMjngZ8Cf0Ryy+YMkodSzczMbBIdcsE3R1330U+8vqnrzvuZkedHxF8BuyLiGuD1wMtyjsnMzMwmUd7JSF/6+0lJLwbmAn6pnZmZ2X4k79s0V0qaD/wVyReXzQYuHH4WMzMzm07y7k3z2XTw+8BhecZiZmZm+ci7N00HSVfeQ7KxRMRFecVkZmZmkyvv2zRfB54ieS/N3pxjMTMzsxzknYwsiYiTco7BzMzMcpR3b5o7Jb0k5xjMzMwsR7lcGZF0PxDp+t8haRPJbRqRvOduWR5xmZmZ2eTL6zbNG3Jar5mZmU0xudymiYhfRMQvgIOBJzLjO4DfySMmMzMzy0fez4ysAXZmxnemZWZmZrafyDsZUUREdSQiKozi1pGkkyQ9JGmjpAuGqbdSUkjqblK8ZmZm1mR5JyObJL1PUlv6835g03AzSCoClwGvBY4ETpd0ZJ16c4D3A3ftg7jNzMysSfJORs4FjgW2AltI3th7zgjzHANsjIhNEdELXA+cXKfeXwMXA3uaF66ZmZk1W25fepZe4TgjIk4b46yLgc2Z8WoSk132cmBpRHxT0kcmFqmZmZntS7ldGYmIMnB6s5crqQD8PfDno6h7jqQeST3btm1rdihmE+L2aVOZ26c1U963aX4g6TOS/oek5dWfEebZCizNjC9Jy6rmAC8Gbpf0KPBy4OZ6D7FGxJUR0R0R3V1dXRPbErMmc/u0qczt05op73fTHJ3+zr6lN4BXDzPP3cARkg4lSUJOA942MHPEU8CB1XFJtwMfjoieJsVsZmZmTZRrMhIRrxrHPP2SzgduBYrA5yLiAUkXAT0RcXOz4zQzM7N9J9dkRNKF9coj4qJ65ZnptwC31JQ1Wtbx443PzMzM9r28b9PsygzPIHlnzYM5xWJmZmY5yPs2zaey45L+juT2i5mZme0n8u5NU2smSe8YMzMz20/k/czI/SS9ZyB5GLWLwT1rzMzMbJrL+5mRN2SG+4HHIqI/r2DMzMxs8uWSjEiaQfJemucD9wNXOQkxMzPbP+X1zMg1QDdJIvJa4FPDVzczM7PpKq/bNEdGxEsAJF0F/FdOcZiZmVnO8roy0lcd8O0ZMzOz/VteV0aOkvTbdFhAZzouICLigJziMjMzs0mWSzISEcU81mtmZmZTz1T70jMzMzPbzzgZMTMzs1w5GTEzM7NcORkxMzOzXDkZMTMzs1w5GTEzM7NctWQyIukkSQ9J2ijpgjrTPyRpg6T7JH1X0vPyiNPMzMxG1nLJiKQicBnJO22OBE6XdGRNtR8D3RGxDLgR+OTkRmlmZmaj1XLJCHAMsDEiNkVEL3A9cHK2QkTcFhHPpKM/ApZMcoxmZmY2Sq2YjCwGNmfGt6RljbwL+Ld9GpGZmZmNWysmI6MmaTXQDVzSYPo5knok9Wzbtm1ygzMbgdunTWVun9ZMrZiMbAWWZsaXpGWDSHoN8FHgjRGxt96CIuLKiOiOiO6urq59EqzZeLl92lTm9mnN1IrJyN3AEZIOldQOnAbcnK0g6aXAP5EkIo/nEKOZmZmNUsslIxHRD5wP3Ao8CNwQEQ9IukjSG9NqlwCzga9IulfSzQ0WZ2ZmZjkr5R3AeETELcAtNWUXZoZfM+lBmZmZ2bi03JURMzMzm16cjJiZmVmunIyYmZlZrpyMmJmZWa6cjJiZmVmunIyYmZlZrpyMmJmZWa6cjJiZmVmunIyYmZlZrpyMmJmZWa6cjJiZmVmunIyYmZlZrpyMmJmZWa6cjJiZmVmunIyYmZlZrpyMmJmZWa6cjJiZmVmuSnkHMB6STgL+ASgCn42IT9RM7wCuBVYA24FTI+LR8a5v795+fvNML/2VYFZ7kb39FforwYxSgXJAX7lCqSBmtBXYubdMqSAKgqJEfzp9dkeRPX3JfKWC6CgVqETQV46BsnmdBX6zq8y8ziI79yZ124oFSoLd/RVmlApUgP5yhYKEBBEwp7PAjl1l5s0ssnPPs7FVAg6YIZ7cPTTe9mKBgmBPf4W2gigVC+zuKzNnRpHdvc/GObM9WU419rmdRXbtrQyK+cndFSRRFLSVCvRXgr7+Ch1tBXr7KvRllvXbPWU624oA9JYrCJCgVEjy4r5yhc724sAy2koFSgWxu7dMe6nIwlntFAoa13Hs76/w+M699JUrtBULLJrdQanU+vl4b28/O3b30VcJypWgrShKEh1tGmhH1Tb3TG+ZYkEUClCpQFtRgOgtV6hUYmBaW6HA3v4K5bSsrSj6ysny20sFBJSKoj9tvxKA6CtXkvqFpH32l4P+CIoavIxiQek5I0oFBtpoW0EUCmJvf2Ug5nIlBrato1QgCCoVKAgqAR2lAnvSWEsF0V4qML8zaSfbd/XS2z9826lUYlC9+Z1tPLG7l7195YHzjIBSQewtV+hoK3LgrI4R22GlEjy5u5fdvWXKEczIzFe7zom0a7PpoOWSEUlF4DLgD4EtwN2Sbo6IDZlq7wJ2RMTzJZ0GXAycOp717d3bz89+s4vzrlvHsYctZPUrnse7v3APXbM7+IuTXshHbryPLTt2s2R+J5efsZzrfvgL7ty0nc+87aX09Vf44A3rB81XrfvPZ3Wzpz8477p1A2VrVq/g4APa+eWOvYPKL1m1jK/es5U3L188aH0Xr1zGNXf+nPee8AIWzW7jl08k81Vje8HvzGLT9sFl2fkvWbWMT/77Q2zbuZdLVi1j8/ZdvGjxvCExLZxV4tQr7+J9rzq87vSOIrzzmnWDtrne+tasXsGDW59k6cJZg8o/9dajmNFW4D1f/PGIca49s5sXHjRnzB/c/f0VfvrY05ybif2K1Sv43YPmtHRC0tvbzy+e3M1vnt47aJ99/p2/z2M7K4OOVbZ9XrxyGXc89Birfv+5Q+b99KlHc0BniXde3cOWHbs58chFnP/qIwa132ve+ftUAp7c1cva/9jEOccdzge+fO/A9Mve9lIKEudl5rn8jOV85nsP860Nj7NkfieXnnIUixd0sn1n35D2Xj3eV6xeQblS4T1f/HFm2cu57LaHefuxh3LHQ4/x+qMWD4rt0lOOYvfcMrv2lDn78z0D5fXaTqUSPPTY05x97bPb+r4TXjConVTPs3e88tBRt8NKJXh0+y4e++2eQft27ZndHNE1m4e37RxYZ6PYzPYnrfgpfAywMSI2RUQvcD1wck2dk4Fr0uEbgRMkjess/80zvQMflGcfd9jAh965xx8+8CEDsGXHbt79hXs4+7jD2LJjNzt29fHBG9YPma9ad8uOPQPLrZadd9069mYSlGr5R268j7OPO2zI+v7XTfexcsVSzrtuHf0VBuarxranN4aU1S733OMPHxg+9oiuujGVK2LLjt0Np8/qaBuyzfXWd9516zj2iK4h5X/+lfU8satvVHGefW0P23f1jvk4Pr5z78AfmOpyz71uHY/v3DvmZU0l23b1suWJ3UP2WTk05Fhl2+f/uuk+VnU/t+68H/jyvWzdsWegbOWKpUPab4TY8sRuPnjDelauWDqQiFSnP7GrbyARya5/5YqlA+MfvGE95TJ123v1eJ973bqBtlGd/p4vJsupbkNtbB+8YT29/TGQiFTL67Wd7bt6B5KC6rbWtpPqeTaWdrh9Vy+/2P7MkH179rU9PL5z76B1TqRdm00XrZiMLAY2Z8a3pGV160REP/AUsLB2QZLOkdQjqWfbtm11V9ZfiYEPjWJBA8PzOtsGhgcC2bGbYvqfzcz2Yt35qrLTs/Nn11e73Hrl1Tiy8w1XVm/+6nC5wborEQANp/dXYsg2NVpfo2XMbC+OOs7e/jJj1Veu1I+9XBnzsibLaNtnvbZUEMO2z+pwo3ZYPR5Q/5gU9Ozxrje90XKrx7E6Xo767SF7vLOxZKcPd1402v7attPbXx5Ub7j2N5Z22NtfbnyON2iL42nXeRpN+zQbrVZMRpomIq6MiO6I6O7q6qpbp1QQS+Z3Askf4+rwk7v7BoarlszvpJz+YX6mt1x3vqrs9Oz82fXVLrdeeTWO7HzDldWbvzpcbLDuQnpRqdH0UvoHLrtNjdbXaBnP9JZHHWd7afAfp9FoKxbqx16cuqfAaNtnvbZUCYZtn9XhRu2wejyg/jGpxLPHu970RsutHsfqeFH120P2eGdjyU4f7rxotP21bae9VBxUb7j2N5Z22F4qNj7HG7TF8bTrPI2mfZqN1tT9JG5sK7A0M74kLatbR1IJmEvyIOuYHTiznTWrVyT3de/YxOVnLE+eN7j9ES5ZtWzgQ6V6T3ztHZtYMr+T+bPauPSUo4bMV627ZP6MgeVWy9asXkFHSUPKL1m1jLV3bBqyvotXLuOmdZtZs3oFpQID81Vjm9GuIWW1y73i9kcGhu98eFvdmIqF5AO/0fRde/uGbHO99a1ZvYI7H942pPxTbz2KBbPaRhXn2jO7WTirfczHcdHsDq6oif2K1StYNLtjzMuaSrpmtbNkQeeQfVZUDDlW2fZ58cpl3Njzy7rzfvrUo1k8f8ZA2U3rNg9pv1KwZEHyfMZN6zbz6VOPHjR9waw21tTMc/kZy7lp3eaB8UtPOYpikbrtvXq8r1i9YqBtVKdf9rZkOdVtqI3t0lOOor0k1v5J96Dyem1n4ax21p7ZPWhba9tJ9TwbSztcOKud5y2cOWTfrj2zm0WzOwatcyLt2my6UKSX4FtFmlz8DDiBJOm4G3hbRDyQqfMe4CURcW76AOtbIuKU4Zbb3d0dPT09daeNpTfNrr3P9lYo4t40tb1pnt5TZkbam6YvvUVSEBQnsTdNf7lCaWy9aXJ/qnC49pntTVOpBKXhetP0lSlqDL1p6vSEqdebpiAIlLTNcfamqfaGKRREb3/SKyfbm6aSrrtRb5pq/M3rTVOhIGp60wQdbYVx9KaBGZn5mtybZkq3z6pDLvjmqJf36CdeP9GQbBz20TEaVftsud40EdEv6XzgVpKuvZ+LiAckXQT0RMTNwFXA5yVtBJ4ATpvIOjs6SizuGN2uWjh7ImuCWTOS33Nnjm2+A6rzdQ6dVl3m6IMYfvK8mtjGsvz5Iyy7ofHOl1EqFXjOvDo7qMW1t5c4qL1++xxrO8rLmNvoKHXNGfnKV6GgIfUWzZl4QIWCWDCro27brbdOs/1ZyyUjABFxC3BLTdmFmeE9wFsnOy4zMzMbu1Z8ZsTMzMymEScjZmZmlisnI2ZmZpYrJyNmZmaWq5br2ruvSNoG/GKcsx8I/KaJ4Uwl03nbYHTb95uIOGkygmlkgu1zX2ulNtJKscL0ap+ttu/Hy9s52Kjap5ORJpDUExHdecexL0znbYPpv32ToZX2YSvFCq0X73Cm07YMx9s5Pr5NY2ZmZrlyMmJmZma5cjLSHFfmHcA+NJ23Dab/9k2GVtqHrRQrtF68w5lO2zIcb+c4+JkRMzMzy5WvjJiZmVmunIyMgaSlkm6TtEHSA5Len5YvkPRtSQ+nv+fnHet4SSpK+rGkb6Tjh0q6S9JGSV+W1LLvOZc0T9KNkn4q6UFJr5hOx26iJD0q6X5J90rqScvq7h8l/jFtF/dJWp5ZztvT+g9LenumfEW6/I3pvGN626ykz0l6XNJPMmX7PL7xtJEGsX5c0tZ0/94r6XWZaX+ZrvchSX+UKT8pLdso6YJMed3zUlJHOr4xnX7IWPZxMzSKOTM99xibYRTbeZakbZnj/ad5xDlR9dpyzfSG59qYRIR/RvkDHAwsT4fnAD8DjgQ+CVyQll8AXJx3rBPYxg8BXwS+kY7fAJyWDl8BnJd3jBPYtmuAP02H24F50+nYNWH/PAocWFNWd/8ArwP+jeT14C8H7krLFwCb0t/z0+H56bT/Susqnfe1Y4zvOGA58JPJjG88baRBrB8HPlyn7pHAeqADOBR4hOSN5MV0+LC0va4HjkznqXteAu8GrkiHTwO+PMltqGHMmTq5xjiJ23kW8Jm8Y23Ctg5pyzXT655rY/3xlZExiIhfRcQ96fDTwIPAYuBkkj90pL/flE+EEyNpCfB64LPpuIBXAzemVVp52+aSnFRXAUREb0Q8yTQ5dvtQo/1zMnBtJH4EzJN0MPBHwLcj4omI2AF8GzgpnXZARPwokk+waxnjvo6IO4AncohvzG2kQayNnAxcHxF7I+LnwEbgmPRnY0Rsiohe4Hrg5BHOy2ysNwInjPUK1ATVjbmmTt4xNsNotnNaGEVbbnSujYmTkXFKLy2+FLgLOCgifpVO+jVwUE5hTdSngb8AKun4QuDJiOhPx7eQJF+t6FBgG/DPSm5DfVbSLKbPsWuGAL4laZ2kc9KyRvtnMbA5M2+1bQxXvqVO+URNRnzNbCPnp5eyP5e53TPWWIc7LwfmSac/ldafLI1irlsnpxibYTTbCbAyPd43Slo6OaFNutHui2E5GRkHSbOBm4APRMRvs9PS/6parouSpDcAj0fEurxj2UdKJJca10TES4FdJJfcB7TqsWuiP4iI5cBrgfdIOi47carvn8mIb4LrWAMcDhwN/Ar4VLPisinpX4FDImIZyRW4a0aov19zMjJGktpIEpEvRMS/pMWPVS9Lpb8fzyu+CXgl8EZJj5Jccnw18A8kl9xKaZ0lwNZ8wpuwLcCWiLgrHb+RJDmZDseuKSJia/r7ceCrJJeiG+2frUD2P71q2xiufEmd8omajPia0kYi4rGIKEdEBVhLsn/HE+t2Gp+XA/Ok0+em9SdLo5jr1skpxmYYcTsjYntE7E1HPwusmKTYJttojvmInIyMQXpf8yrgwYj4+8ykm4HqU/lvB74+2bFNVET8ZUQsiYhDSB4q+15EnAHcBqxKq7XktgFExK+BzZJemBadAGxgGhy7ZpA0S9Kc6jBwIvATGu+fm4Ez0yfpXw48ld7KuBU4UdL89DbEicCt6bTfSnp5eh6dSXP29WTE15Q2UnMf/c0k+7e6/NPSXiaHAkeQPEx7N3BE2nOmneS8vDm9OtPovMzGuorkPJ7Mq1l1Y66pk3eMzTDidtYc7zeSPGM4HTU618ammU/dTvcf4A9ILtHeB9yb/ryO5H7nd4GHge8AC/KOdYLbeTzP9qY5jOSDcSPwFaAj7/gmsF1HAz3p8fsaSW+KaXXsJrBvDiPpEbAeeAD4aFped/+QPDl/GUmPgvuB7syy3pm2l43AOzLl3SR/gB8BPkP6pYtjiPFLJLc3+kiudL1rMuIbTxtpEOvn01juI/kAPzhT/6Ppeh8i08so/Xz5WTrtozXHa8h5CcxIxzem0w/LoS0NiRm4CHjjVIlxkrbzb9NzaT1J8vi7ecc8zu2s15bPBc5Npzc818by429gNTMzs1z5No2ZmZnlysmImZmZ5crJiJmZmeXKyYiZmZnlysmImZmZ5crJyH5K0pskhaTfzTsWm1oklTNvGr233htJM3XfJOnIzPhFkl7ThBjmSXr3OOb7uKQPp8MvV/JW2HuVvKX54yPMe7zSt1Xb9JRp2z+R9BVJM5uwzEMavdF2X5B0taRVI9dsLU5G9l+nA/+Z/jbL2h0RR2d+PjFM3TeRvHUWgIi4MCK+04QY5pG83XUirgHOiYijgReTvOm2aTLfgGqto9q2Xwz0knxfxqj4eO9bTkb2Q+m7df6A5MtrTkvLCpIul/RTSd+WdEs1+5a0QtL30xeo3TqeNzJa65P0CUkb0hd//Z2kY0m+WfKS9L/Nw7P/tUl6VNLfptN6JC1P288jks5N68yW9F1J90i6X1L1zaefAA5P570krfsRSXen6/+/mbg+Kulnkv4TeGEm5EUkX9ZEJF/DviGtf4ykHyp5YeKdmW/lzW5r3TqSzpJ0s6TvAd+VdK2kN2Xm+0JmG2xq+w/g+bVXNiR9uHoVTdLtkj4tqQd4v6SDJH1V0vr059h0tqKktZIekPQtSZ3p/GenbXa9pJuqV2IkvTW9OrNe0h1pWVHSJZk2/mdpuSR9RtJDkr5D0q6nn7y/3c0/k/8DnAFclQ7fSfLOhFXALSQJ6u8AO9KytrROV1r/VOBzeW+Df/Zp+yjz7DcM35se84Uk3w5a/aLEeenvq4FVmXkHxoFHgfPS4UtJvnl0DtAFPJaWl4AD0uEDSb6VU8AhwE8yyz0RuDKdVgC+ARyXtt37gZnAAen8H07nuTBtx18F/gyYkZYfAJTS4dcAN6XDx/PsNw83qnMWybdQVr/p9X8CX0uH5wI/r87nn6n3A+zMtLuvA+fVaWsfBj6eDt8OXJ6Z9mWSF6QCFNNjfgjQDxydlt8ArE6HF2bm/Rvgvenw/cDidLh6Lp0DfCwd7iD5tuhDgbeQvGivCDwHeDJ7zk2XH1922j+dTvISPEheinc6ycn5lUhe4vVrSbel019Icon725IgOSHG/t4BayW7I7m1MSC9RL0HuCp9rmK0z1ZU39dxPzA7Ip4Gnpa0V9I8krcn/z8lbwiukLx6/KA6yzkx/flxOj6b5B0uc4CvRsQzaZwD7weJiIskfSGd720k7fx4kj8g10g6guT1Dm111jdcnW9HxBPpOr6fXlHsAlaSJC39o9w3Nvk6Jd2bDv8HybvGnjPCPF/ODL+a5L1FREQZeErJO45+HhHV5a4jSVAAXizpb0huO84meTcSwA+AqyXdAFRfuHoisCzzPMhckjZ+HPCldH3/nV6Vm3acjOxnJC0gOaFeIilIkosg+e+x7izAAxHxikkK0aagiOiXdAzJCwZXAeeTtKORVN9aWskMV8dLJFfpuoAVEdGn5K3RM+osR8DfRsQ/DSqUPjBC3I8AayStBbZJWgj8NXBbRLxZ0iEk//3WGq7Orpq61wKrSW55vmO4eCx39RLtfgY/slDb/mqPdz3Ztl0GOtPhq4E3RcR6SWeRJMNExLmSXga8HlgnaQVJG39vRNyaWRaSXjeK9bc8PzOy/1kFfD4inhcRh0TEUpJLy08AK5U8O3IQ6UlDcmm+S9IrACS1Sfq9PAK3/Ch5zmhuRNwCfBA4Kp30NMnVifGaCzyeJiKvAp7XYLm3Au9M40DSYkmLgDuAN0nqVPLW4T/OxPx6pZfzSP7DLJNc4p7Ls684P2uYuEaqU3U18AGASJ9LsZbyGLBI0kJJHcAbhqn7XZJbO9VnPOaOsOw5wK8ktZEk3qTzHh4Rd0XEhcA2YClJGz8vrYukFyh5g/YdwKnp+g4GXjW+zZzafGVk/3M6cHFN2U3Ai0juhW8ANgP3kLwKuje9bPiP6YlXAj5N8jZKm56yl7IB/p3ktt7XJc0g+Q/uQ+m064G1kt7Hs6+0H4svAP8q6X6Se+Q/BYiI9Ek1NwAAAQtJREFU7ZJ+kD5Y+G8R8RFJLwJ+mOYXO0nuy98j6cskb0Z9nOTV7lV/Alwq6RmSe/pnRERZ0idJbsF8DPhmg7hGU4c01sckPUjyJmhrMWkifBHJG4S3krbBBt4PXCnpXSTJ7XkMf9v6r4C7SBKOu3g2wb4kvQUokgRnPckzVYcA96RJ9DaS3mpfJbkKuQH4JfDDsW/l1Oe39toASbMjYmd6Kfu/gFdGxK/zjstsKkt7SNwPLI+Ip/KOx6wV+cqIZX0jfaiwHfhrJyJmw1PyBW9XAZc6ETEbP18ZMTMzs1z5AVYzMzPLlZMRMzMzy5WTETMzM8uVkxEzMzPLlZMRMzMzy5WTETMzM8vV/weyoKhCPT4YVgAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<Figure size 540x540 with 12 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "import seaborn as sns\n",
    "sns.pairplot(df[['Age', 'EstimatedSalary', 'Purchased']])"
   ]
  }
 ],
 "metadata": {
  "celltoolbar": "Slideshow",
  "kernelspec": {
   "display_name": "Python 3",
   "language": "python",
   "name": "python3"
  },
  "language_info": {
   "codemirror_mode": {
    "name": "ipython",
    "version": 3
   },
   "file_extension": ".py",
   "mimetype": "text/x-python",
   "name": "python",
   "nbconvert_exporter": "python",
   "pygments_lexer": "ipython3",
   "version": "3.5.6"
  },
  "varInspector": {
   "cols": {
    "lenName": 16,
    "lenType": 16,
    "lenVar": 40
   },
   "kernels_config": {
    "python": {
     "delete_cmd_postfix": "",
     "delete_cmd_prefix": "del ",
     "library": "var_list.py",
     "varRefreshCmd": "print(var_dic_list())"
    },
    "r": {
     "delete_cmd_postfix": ") ",
     "delete_cmd_prefix": "rm(",
     "library": "var_list.r",
     "varRefreshCmd": "cat(var_dic_list()) "
    }
   },
   "types_to_exclude": [
    "module",
    "function",
    "builtin_function_or_method",
    "instance",
    "_Feature"
   ],
   "window_display": false
  }
 },
 "nbformat": 4,
 "nbformat_minor": 2
}